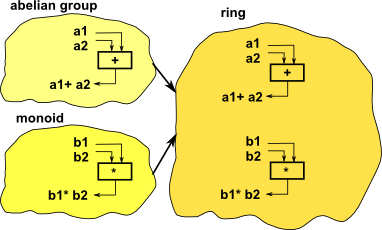
A ring is a rich and interesting mathematical structure. It is important, not least because it is the structure of our most common algebras such as the integers.
A ring is a concept similar to a group, that is a set together with an operation on that set, except that a ring has two operations.
These two operations are represented by addition and multiplication.
What makes a ring interesting, that is more than just two groups glued together, is the way the two operations interact with each other. This interaction between the two operations is defined by the distributive laws.
Axioms
| axiom | addition | multiplication | both |
|---|---|---|---|
| associativity | (a+b)+c=a+(b+c) | (a*b)*c=a*(b*c) | |
| commutativity | a+b=b+a | not required (see field) | |
| distributivity | a*(b+c)=a*b+a*c (a+b)*c=a*c+b*c |
||
| identity | a+0 = a 0+a = a |
not required (see field) | |
| inverses | a+(-a) = 0 (-a)+a = 0 |
not required (see field) |
Note: it is not necessary that multiplication commutes or has a identity element or inverse. For that we mode to a more specific type of field known as a 'field', see this page.
Why do these particular rules produce such an interesting and important mathematical structure? The theory of rings seems less orderly than the theory of groups and some of the concepts seem to come out of nowhere and I find it hard to see why a particular concept has been used rather than some other.
The best answer I can come up with goes along these lines: with an additive group the generator <x> produces the additive part of the integers, if we imagine a similar generator <x> on a ring, that is we generate every combination of + and * on 'x' then we get a polynomial:
a0+ a1 x + a2 x2+ a3 x3+ a4 x4...
Ideals
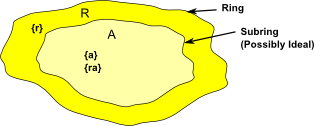
A is ideal if, for every r
R and every aA,
- ra is in A (right ideal)
- ar is in A (left ideal)
- ra & ar is in A (two sided deal)
i.e. A 'absorbs' elements from R
Generating Ideals
<a> = { ra | rR} = an ideal of R called the principle ideal generated by a.
<a1,a2…an> = { r1a1,r2a2…rnan | riR} = an ideal of R generated by a1,a2…an.
So an ideal must be defined relative to some larger ring. We cannot just define <a> on its own without specifying this container.
For instance this containing ring may be:
,Q,Z,N: The reals, rationals, integers and so on.- 3Z, Z3: Some subset of the above.
- [x],Z[x]: The set of all polynomials with, say, real or integer coefficients.
- Any other ring, possibly a finite ring.
Test for being an Ideal
- a-bA whenever a,bA
- ra and ar are in A whenever aA, rR.
Example 1
| Ideal | Containing Ring |
|---|---|
| <3> | Z |
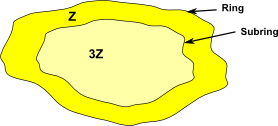
<3> = {3r | rZ}=3Z
where 3Z = 0,3,6…
Since 3Z is a multiple of 3, when multiplied by an integer it is still a multiple of 3.
Example 2
| Ideal | Containing Ring |
|---|---|
| <x> | [x] |
[x] = set of all polynomials with real coefficients
<x> = set of all polynomials with constant term = 0
Factor Rings
R/A = { r + A| rR} = Factor Group (set of cosets).
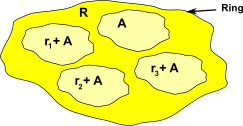
Example 3
Z/3Z = { r + 3Z| rZ} = { 0 + 3Z,1 + 3Z,2 + 3Z}= modulo 3 arithmetic
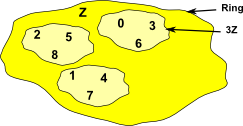
| Z | …-2,-1,0,1,2… |
| 3Z | …-6,-3,0,3,6… |
| 3Z+1 | …-5,-2,0,4,7… |
| 3Z+2 | …-4,-1,0,5,8… |
Notation
| notation | description |
|---|---|
| Q[x] | The set of all polynomials in the variable x with rational coefficients. |
| [x] |
The set of all polynomials in the variable x with real coefficients. |
| Q[x]/<x²+1> | The smallest structure (field) that contains Q and also has a root of the polynomial x²+1. The elements of Q[x]/<x²+1> are not polynomials but equivalence classes of polynomials. |
| <a> | an ideal of R called the principle ideal {ra | r |
| Q(√2) | The smallest field outside Q that contains √2 (the splitting field) |
| Q(√2,√3) | The smallest field outside Q that contains √2 and √3 (the splitting field) |
| C=(i) = [x]/<x²+1> |
The complex numbers are the smallest extension of the field of real numbers which includes i (or i is adjoined to) |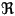
[Q(√2):Q]=2 |
degree of the extension. This is the number of terms required for a general element such as: a + b√2 |
| p(x) | a polynomial over x |
