Vector Field
A vector field has a vector value for every point in a space:
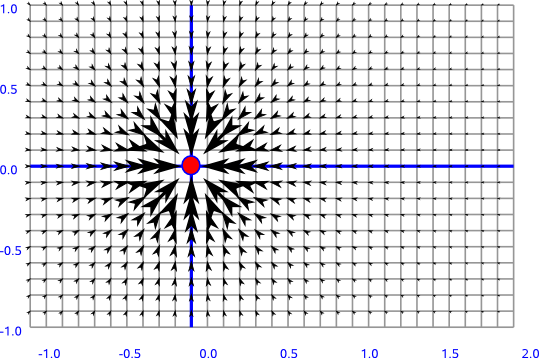
For instance a force field like gravity, if we have a very large mass at the origin, then we can plot the gravitational field, as in the diagram above. Its difficult to find a suitable way to show this, especially in 3 dimensions, an alternative might be to plot lines of constant field force.
Scalar Field
A scalar field gives a scalar value for every point in the space.
we could represent how some scalar quantity, for example temperature, is defined for each point in the space.
We could define a function to show this, temp = f(x,y,z)

One way to illustrate this is to join up all the points with the same values such as contour lines, or isothermals, or isobars, or whatever appropriate to the scalar quantity.
Relationship between Scalar and Vector Field
On the following diagram the height (y-dimension) shows the scalar value.
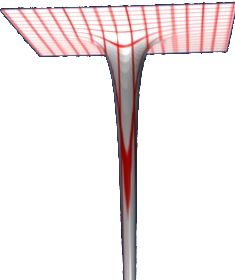
We can relate this to the vector field example above by choosing the scalar to represent potential, in this case energy potential. In this case the scalar and vector fields are related by:
work = ∫ F•dx
or its inverse:
F = grad( work)
where:
- ∫ = line intergral
- F = force
- work = potential energy
- • = dot product
- dx = infinitesimal distance
- grad = grad function
We can generalise this to other cases as follows:
grad converts a vector field to a scalar field representing the differential 'slope' of the vector field.
or its inverse:
the line intergral converts a scalar field to a vector field.
Covector Field
Covectors are dual objects to vectors. In the section about tensors we thought about them being the rows in matrix made up of columns representing the basis vectors.
In terms of fields, if,
- v is a vector field.
- c is the corresponding covector field.
- s is a scalar field.
then:
v • c=s
that is the dot product of the vector field and the covector field is a scalar field.
1-form is a covector field.
Tangent Field
The limiting space when small neighbourhoods of the manifold are taken resulting in a flat n-dimensional space.
Divergence
We get a scalar field from a vector field by using the divergence as shown on this page.
See Also
This page explains how we can represent fields using different types of algebras.

