Groups are usually defined over a set but in the case of Lie groups they are defined over manifolds. That is like taking a group, unplugging it from the set structure and instead plugging in the manifold.
So a Lie group is a combination of infinite groups and calculus. For example 'infinitesimal elements' allow us to build rotations by integrating some infinitesimal rotation. A group that has infinitesimal generators is called a continuous group.
It is useful to be able to linearise the group, for instance taking the exponent of the group, this linearised version is known as its Lie algebra (described on this page). Note that this takes a group with one operation and creates an algebra with both a addition and a multiplication operation.
Lie groups turn up when we study a geometric objects with a lot of symmetry, such as a sphere, a circle, or flat spacetime. Because there is so much symmetry, there are many functions from the object to itself that preserve the geometry and these functions become the elements of the group. Discrete groups can also be used to keep track of symmetries.
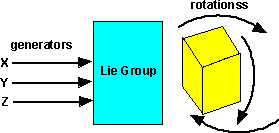
A group which contains an infinite continuum of elements. Yet its structure is delineated by a finite number of elements, known as generators, from which the elements are obtained. Such as rotation group where we can build rotations by integrating infinitesimal rotations. Functions from the group preserve symmetry and these functions become the elements of the group.
For example, if we are considering rotations in 3 dimensions, we can use 3 generators:
- rotation about the x-axis.
- rotation about the y-axis.
- rotation about the z-axis.
to generate all possible rotations.
Lie Group in Group Theory Terms
When we looked at the categorisation of groups we saw that Lie groups, along with cyclic, alternating and sporadic groups, are finite simple groups which means that they can't be created from products of other families of groups. In this sence they are fundamental so it may be worth investigating Lie groups in the same way that we looked at these other types of group before we investigate the geometric, topology and calculus aspects of these groups.
So how can a 'finite' group say anything about continuous symmetries? When we looked at these other types of groups we saw how we could investigate 'step' movements in terms of 'permutations' we will now replace these permutations by transformations:
|
Symmetric GroupEvery finite group can be represented by a permutation which maps a set of points onto itself (rearranges the points). Here we represents a finite group such as a cyclic or alternating group. |
||||||||
|
Lie GroupThe Lie group can still be finite, in that there can still be a finite number of group elements, but now each group maps |
||||||||
Lie AlgebraWe can represent this action (transformation) by square matricies |
Lie Group defined in group theory terms
To show this in a Cayley table we would need to include negative signs in the table, for example, consider the group of complex numbers with the operation of multiplication,
a*b |
b.1 | b.i |
| a.1 | 1 | i |
| a.i | i | -1 |
However this is not a valid Cayley table as we have been using for other finite groups in that -1 appears in the body of the table but is not in the row or column identifiers. To make this into a valid Cayley table we need to have rows and columns for -1 and -i. We can easily do this by replacing the rows and columns as follows:
| 1 is replaced by: |
|
||||
| -1 is replaced by: |
|
||||
| i is replaced by: |
|
We then get a valid Cayley table:
a*b |
b.1 | b.-1 | b.i | b.-i |
| a.1 | 1 | -1 | i | -i |
| a.-1 | -1 | 1 | -i | i |
| a.i | i | -i | -1 | 1 |
| a.-i | -i | i | 1 | -1 |
This now shows that it is a valid group. However, for most purposes, it is easier to use the smaller table with minus entries in the body of the table but not row and column headings represning the minus entries.
So for:
- a Lie group over real numbers the Cayley table needs to have double the number of elements as it has dimensions.
- a Lie group over complex numbers the Cayley table needs to have four times the number of elements as it has dimensions.
and so on.
So what type of group tables do we end up with? how does it differ from cyclic or alternating groups?
| Lie group (over reals) | Lie group (over complex) | |||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
What this is showing is that we are combining two permutations (permutation of permutation). The first is the change of sign (in the case of reals) or multiplication by 'i' (in the case of complex). Then as a second stage we permute these.
Symmetry in Lie Group
If a given law is symmetric, or invariant, with respect to a set of actions that form a lie group, then noethers theorem tells us there is a conserved physical quantity associated with each generator of the lie group.
| type | name of group | constraints | |||||||
|---|---|---|---|---|---|---|---|---|---|
| preserve volume |
preserve orientation |
preserve distance |
preserve angles |
determinant | |||||
| GL(R) | general linear | ||||||||
| SL(R) | special linear | yes | yes | 1 | |||||
| O | orthogonal | yes | |||||||
| SO | special orthogonal | yes | yes | 1 | |||||
| E | Euclidean (rigid motions) | yes | yes | ||||||
| GL(C) | general linear | ||||||||
| SL(C) | special linear | 1 | |||||||
| U | unitary | ||||||||
| SU | special unitary | 1 | |||||||
| Sp(2n) | symplectic | ||||||||
Rotation Groups:
| number of generators | ||
| R(2) | The group of rotations in 2 real dimensions | 1 |
| R(3) | The group of rotations in 3 real dimensions | 3 |
| R(4) | The group of rotations in 4 real dimensions | 6 |
| U(1) | The group of rotations in 1 complex dimension | 1 |
| SU(2) | The group of rotations in 2 complex dimensions S=special 2 complex dimensions = quaternion ? Almost identical properties to R(3) except repeats after 720 degrees rather than 360 degrees. |
3 |
| SU(3) | The group of rotations in 3 complex dimensions | 8 |
| SO(3) | The Orthogonal group in 3 dimensions is denoted by O(3). SO(3) is the Special Orthogonal group which is a subgroup of O(3) with determinant +1. | |
Lie Algebra
It is useful to map the 'generator space' to 'flat space' locally this is the tangent plane. If we extend the tangent space at the identity element we get the 'logarrithm' of the lie group.

 n->
n->
