Maths - Rotational Lie Group Theory

Rotation Groups

On this page consider groups which represent rotations.

As we have seen on this page part of the definition of groups is that they contain objects and a binary operation on those objects, in the rotational case:

The objects are rotations.
The binary operation is the sequential application of two rotations.

These types of groups are defined in a way that is independent of the number of dimensions and also independent of the algebra used to represent it. However, for any given dimension, we need to have a mapping back to an appropriate algebra to do calculations. This definition often combines various types of algebra such as matrices who's elements are complex numbers although we could reverse this and use complex numbers who's elements are matrices.

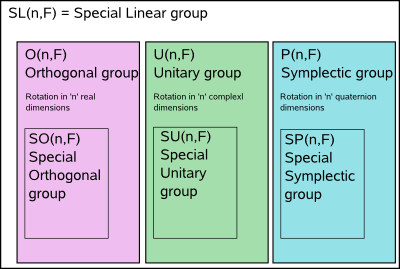
These rotation groups are all subsets of the SL(n,F) Special Linear group.

Although these groups all represent rotations, around the origin, they may have different properties, for instance, each object in the group may correspond exactly to one rotation. That is, these is a 1:1 correspondence between objects in the group and rotations, this is known as a single cover. A double cover is where there are two objects which correspond to each rotation, this is related to spinors which is 1:1 but a complete rotation is 720° and a 360° rotation will multiply the object by -1.

group types

These might be mapped to different algebras if different ways, for example, a rotation in 3D can be represented by either:

A 3×3 matrix of real numbers.
A 2×2 matrix of complex numbers.
A 1×1 matrix of quaternions. (i.e. a single quaternion).

I think the top one could represent a single cover and the other two are examples of a double cover.

These contain more scalar values than there are degrees of freedom. For instance 3D rotations have 3 degrees of freedom but the groups have 9, 8 or 4 scalar numbers, so we need to have various restrictions to reduce the degrees of freedom:

	The orthogonal group, SO(n)	The unitary group, SU(n)	The symplectic group, Sp(n)
matrix restrictions	T T^t = T^t T = 1 determinant = +1	T T^* = T^* T = 1	T T^* = T^* T = 1
number restrictions		unit length	unit length

The orthogonal group, SO(n)

The unitary group, SU(n)

The symplectic group, Sp(n)

matrix restrictions

T T^t = T^t T = 1

determinant = +1

T T^* = T^* T = 1

number restrictions

unit length

where:

U^* = the conjugate transpose of U (the conjugate transpose is also known as adjoint matrix, adjugate matrix, hermitian adjoint or hermitian transpose). The conjugate matrix is the complex conjugate of each element.

For rotation groups, such as SO(3), the elements and group law is as follows:

elements: set of all rotations of sphere
group law: composition of rotations.

There are at least 3 classical groups types associated with rotations:

group type	matrix definition	clifford algebra definition
SO(n,) The group of rotations in 'n' real dimensions. The special orthogonal group in 'n' dimensions over the real numbers. Represents a single cover of rotations in 'n' dimensions of Euclidean space (all dimensions square to +ve).	An n×n matrix where each element of the matrix is a real number The determinant of the matrix is +1. The transpose of the matrix multiplied by the original matrix = identity.
SU(n) The group of rotations in 'n' complex dimensions. The special unitary group in 'n' dimensions. S=special (no reflections) U=unitary=size preserving n=number of complex dimensions Represents a double cover of rotations in 'n²-1' dimensions. Or a single cover of rotations where a complete rotation is 720°.	An n×n matrix where each element of the matrix is a complex number The determinant of the matrix is +1.
SP(n) The group of rotations in 'n' quaternion dimensions. The symplectic group in 'n' dimensions	An n×n matrix where each element of the matrix is a quaternion The determinant of the matrix is +1.
G2,F4,E6,E7 and E8 The group of rotations in 'n' octonion dimensions. (only works for 5 values of n) Can this be a group because a group must be associative and octonions are not associative. It can be done but only in these exceptional cases.	An n×n matrix where each element of the matrix is an octonion The determinant of the matrix is +1.

group type

matrix definition

clifford algebra definition

SO(n,)

The group of rotations in 'n' real dimensions.

The special orthogonal group in 'n' dimensions over the real numbers.

Represents a single cover of rotations in 'n' dimensions of Euclidean space (all dimensions square to +ve).

An n×n matrix where each element of the matrix is a real number

The determinant of the matrix is +1.

The transpose of the matrix multiplied by the original matrix = identity.

SU(n)

The group of rotations in 'n' complex dimensions.

The special unitary group in 'n' dimensions.

S=special (no reflections)
U=unitary=size preserving
n=number of complex dimensions

Represents a double cover of rotations in 'n²-1' dimensions.

Or a single cover of rotations where a complete rotation is 720°.

An n×n matrix where each element of the matrix is a complex number

The determinant of the matrix is +1.

SP(n)

The group of rotations in 'n' quaternion dimensions.

The symplectic group in 'n' dimensions

An n×n matrix where each element of the matrix is a quaternion

The determinant of the matrix is +1.

G2,F4,E6,E7 and E8

The group of rotations in 'n' octonion dimensions. (only works for 5 values of n)

Can this be a group because a group must be associative and octonions are not associative. It can be done but only in these exceptional cases.

An n×n matrix where each element of the matrix is an octonion

The determinant of the matrix is +1.

Special Orthogonal Groups

Here is more detail on special orthogonal groups in particular dimensions. These groups are Lie groups and the number of generators is given:

group type

number of generators

n!/(n-2)!*2

matrix definition

clifford algebra definition

SO(1,)

SO(2,)

The group of rotations in 2 real dimensions. Single cover of rotation in 2 dimensions

cos(θ)	-sin(θ)
sin(θ)	cos(θ)

C (unit length)

SO(3,)

The group of rotations in 3 real dimensions. Single cover of rotation in 3 dimensions

1 - 2qy² - 2qz²	2qxqy - 2qzqw	2qxqz + 2qyqw
2qxqy + 2qzqw	1 - 2qx² - 2qz²	2qyqz - 2qxqw
2qxqz - 2qyqw	2qyqz + 2qxqw	1 - 2qx² - 2qy²

rotation in terms of quaternion.

H (unit length)

Operation is sandwich product. (otherwise this would give a dual cover as SU(2) does.

SO(4,)

The group of rotations in 4 real dimensions

The special orthogonal group can also be defined over the complex numbers: SO(n,C) is this the same as SU(n)???

Rotations in Minkowski Space

So far we have been talking about Euclidean space, that is, a space where all dimensions square to positive. If we want rotation in a space where p dimensions square to +ve and q dimensions square to -ve, Minkowski space, then we can extend SO(n) to SO(p,q) (defined with two numbers, p is the number of dimensions which square to +ve,q is the number of dimensions which square to -ve). The orthogonal group for any symmetric quadratic form Q with the group of matrices A which preserve Q, is denoted O(p,q).

	matrix definition	clifford algebra definition
Clifford algebra of the Euclidean space R3	Mat(2,C)	Cl(3)
Clifford algebra of the Minkowski space R 1,3	Mat(2,H)	Cl(1,3)
Clifford algebra of the Minkowski space R 3,1 The Lorentz group is O(3,1)	Mat(4, )	Cl(3,1)

matrix definition

clifford algebra definition

Clifford algebra of the Euclidean space R3

Mat(2,C)

Cl(3)

Clifford algebra of the Minkowski space R 1,3

Mat(2,H)

Cl(1,3)

Clifford algebra of the Minkowski space R 3,1

The Lorentz group is O(3,1)

Mat(4,

)

Cl(3,1)

Special Unitary Groups

What exactly does it mean "rotation in 'n' complex dimensions"? For instance, since a complex number has one real and one imanginary number, does rotation in 2 complex dimensions mean rotation in a space where 2 dimensions square to +ve and two square to -ve? or since its represented by quaternions does it mean rotation in a space where 2 dimensions square to +ve and two square to -ve? I don't think so, I think there is some mapping into euclidean space implied.

Here is more detail on special unitary groups in particular dimensions. These groups are Lie groups and the number of generators is given:

group type	number of generators (n²−1)	matrix definition	clifford algebra definition
SU(1) The group of rotations in 1 complex dimension. This is a trivial group having only one element.	1
SU(2) The group of rotations in 2 complex dimensions 2 complex dimensions = quaternion ? Almost identical properties to R(3) except repeats after 720 degrees rather than 360 degrees. Represents double cover of rotations in 3 dimensions: Spin(3)	3	{UMat(2,C) \| U†U=I,det U=+1}	H (unit length) Cl⁺3
SU(3) The group of rotations in 3 complex dimensions. Represents double cover of rotations in 8 dimensions. The analog of the Pauli matrices for SU(3) are Gell-Mann matrices.	8

I think that, for the SU(n) groups the matrix is used differently than the matrices in the SO(n) group. In the SU case the matrix might be used in sandwich form v' =M v M† to represent classical rotations or v' =M v to represent spinors.

Exceptional Groups: G2,F4,E6,E7 and E8

Can this be a group because a group must be associative and octonions are not associative. It can be done but only in these exceptional cases.

group	description	dimension
G2	The automorphism group of the octonions. SO(O) ~= SO(8) is the rotation group of the octonions, viewed as a real vector space. The map from Spin(8) to SO(O) is 2:1, but when we restrict it to G2 we get a 1:1 map.	14
F4	isometry group of the projective plane over the octonions. F4 ~= SO(O)O³ ~= SO(O)O²	52
E6	the isometry groups of projective planes over the bioctonions, CO	78
E7	the isometry groups of projective planes over the quateroctonions, HO	133
E8	the isometry groups of projective planes over the octooctonions, OO	248

Background Information

Rotations of objects in 3 dimensional space can be combined so that two or more rotations can be combined to produce a single rotation which is equivalent to any sequence of rotations. This site covers several methods for representing and concatenating rotations, for example:

Since these notations can be used to represent the same physical operation (rotations in 3D) is is not surprising that they have common properties. It may be useful to express the properties of these operations independently of the details of the above notations and so the Rotation group is useful.

Three dimensional rotations are transformations which can be used to transform say a point from one 3 dimensional coordinate to a possibly different coordinate, indeed it can transform whole sets of points such as a solid object. Rotations have properties such as preserving length and angles.

Relationship to Spinors


S₁
S₂	C
S₃	H
S₄^±	H
S₅	H²
S₆	C⁴
S₇	O
S₈^±	O
S₉	O²
S₁₀	(CO)²
S₁₁	(HO)²
S₁₂^±	(HO)²
S₁₃	(H²O)²
S₁₄	(C⁴O)²
S₁₅	(OO)²
S₁₆^±	(OO)²

Relationship between vectors and spinors holds true in 3,4,6 and 10 dimensions (one more than the dimensions of ,C,H and O which gives the following isomorphisms:

SL(2, ) ~=SO(2,1)
SL(2,C) ~=SO(2,3)
SL(2,H) ~=SO(2,5)
SL(2,O) ~=SO(2,9)

Special Displacements

SE(3)

group of special displacements

They form the even Clifford subalgebra C⁺(P³)

EuclideanSpace

home

grid image

Symmetry

Group Theory

Lie Group

Groups are usually defined over a set but in the case of Lie groups they are defined over manifolds. That is like taking a group, unplugging it from the set structure and instead plugging in the manifold.

So a Lie group is a combination of infinite groups and calculus. For example 'infinitesimal elements' allow us to build rotations by integrating some infinitesimal rotation. A group that has infinitesimal generators is called a continuous group.

It is useful to be able to linearise the group, for instance taking the exponent of the group, this linearised version is known as its Lie algebra , this takes a group with one operation and creates an algebra with both a addition and a multiplication operation.

Lie groups are explained on this page.
Lie algebra is explained on this page.

Maths - Group Theory - Rotational Lie Group Types

Rotation Groups

Special Orthogonal Groups

Rotations in Minkowski Space

Special Unitary Groups

Exceptional Groups: G2,F4,E6,E7 and E8

Background Information

Relationship to Spinors

Special Displacements

Spinor

EuclideanSpace

Symmetry

Group Theory

Lie Group