Represention Theory
Represention theory is a specialisation of group theory that is restricted to vector spaces.
Classification of Groups
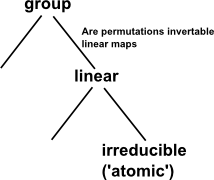
Conjugacy Classes
There is a 1:1 correspondence between transitive actions and conjugate classes.
| Conjugacy classes of subgroups | Transitive actions of G |
| collection of subgroups conjugate to some given subgroup. | Transitive = one orbit Any action = sequence of transitive actions. |
Actions
We can look at the concepts that we used for permutations, now that we are restricting ourselves to linear maps:
Stabiliser
Subgroup of G consisting of all elements h such that:
h x = x
h is the stabiliser of x
Orbit
Centre
Mat(n,F)
May be any n×n matrix containing R, C, H or O elements.
- Mat(n, R)
- Mat(n,C)
- Mat(n,H)
- Mat(n, O)
The definitions don't make it totally clear whether Mat(2,C) is any 2×2 matrix whose elements are C or is it the matrix algebra over the centre of C
From Wikipedia: "The term center or centre is used in various contexts in
abstract algebra to denote the set of all those elements that commute with
all other elements".
SL(n, F) The Special Linear Group
Consisting of n×n matrices where each element is of type 'F' with determinant =1.
