The notation: for Lie multiplication is to put both operands in square brackets:
[x y]
This is known as the lie bracket.
There should only be two terms in the square brackets because the multiplication is not associative.
Identities
The identities for the lie bracket are:
| [x y] + [y x] = 0 | anti-commutative |
| [x [y z]] + [y [z x]] + [z [x y]] = 0 | Jacobi identity : anti-associative : anti-symmetry |
The first indentity is equivalent to
- [x x] = 0
- and [x y] is bilinear
(for more about bilinear form see this page)
This equivilance is because:
[x+y x+y] = [x x] + [x y] + [y x] + [y y] = 0
since:
- [x x] = [y y] = 0
- [x y] + [y x] = 0
Conversion between Lie Algebra and Associative Algebra
We can convert elements of associative algebra to lie algebra by using the bilinear multiplication:
[a,b] = ab - ba
Where:
a,b are elements of an associative algebra
Geometric Interpretation of Lie Algebra
Tangent spaces of differential manifolds whose points can be multiplied together.
Example - Vector Cross Product
An example of a Lie algebra is the vector cross product, this applies to vectors in three dimensions.
When we cross multiply two 3D vectors A and B we get:
x = Ay * Bz - By * Az
y = Az * Bx - Bz * Ax
z = Ax * By - Bx * Ay
where:
- Ax,Ay and Az are the components of vector A
- Bx,By and Bz are the components of vector B
- x,y and z are the resulting components
We can summarise the components of this vector cross product in the following multiplication table:
a×b |
b.e1 | b.e2 | b.e3 |
| a.e1 | 0 | e12 | -e31 |
| a.e2 | -e12 | 0 | e23 |
| a.e3 | e31 | -e23 | 0 |
The Baker-Campbell-Hausdorff formula
This formula links Lie groups to Lie algebras by expressing the logarithm of the product of two Lie group elements as a Lie algebra.
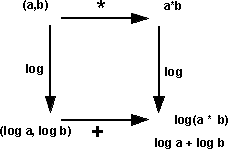 |
When we are dealing with real numbers we can replace multiplication with addition by taking a logarithm. So can we do this with more complicated quantities shuch as those representing 3 dimensional rotations? |
The answer is yes, but its a bit more complicated for this type of quantity. It works well for representing 2D rotations using complex numbers. A rotation of θ can be rpresented by the complex number: cos(θ) + i sin(θ)
To combine two rotations θ1 and θ2 we can multiply the corresponding complex numbers:
(cos(θ1) + i sin(θ1)) * (cos(θ2) + i sin(θ2))
This can be simplified since:
eiθ = cos(θ) + i sin(θ)
so the resulting rotation is:
eiθ1 * eiθ1 = ei(θ1+θ2)
It would be nice if we could do the same for 3D rotations using quaternions, however there is a problem because quaternions and 3D rotations do not commute and so we cannot represent them by addition which is always commutative. We therefore have to use something more complicated than pure addition, we now require an infinite series the first few terms are:
ln(eA eB)
= A + Y + 1/2 [A,B]
+ 1/12 ([A,[A,B]] - [B,[A,B]])
- 1/24 [B,[A,[A,B]]] +...