We start by reviewing linearity and then extend this to bilineararity.
Linear Multiplication.
To represent linear space we only need two operations:
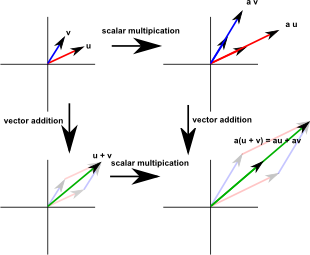
- Vector addition: to add two vectors we take the start of the second vector and move it to the end of the first vector. The addition of these two vectors is the vector from the start of the first vector to the end of the second vector.
- Scalar multiplication changes the length of a vector without changing its direction. That is we 'scale' it by the multiplying factor. So scalar multiplication involves multiplying a scalar (single number) by a vector to give another number.
If the space is linear we have:
a*(v +u) = a*v + a*u
where:
- v & u are vectors
- a is a scalar
In other words the two operations are distributive.
Bilinear Multiplication
To have bilinearity we need to include a multiplication where both operands are vectors.
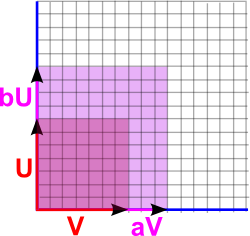
For a bilinear multiplication, if we keep one of the vectors constant and then the other vector varies in a linear way, as defined above.
For example, in the diagram above we take the product as the area formed from the two vectors. So if the area formed from V and U is V•U then if we multiply V by a scalar value 'a' we get the area a*V•U, so,
(a*V)•U = a*(V•U)
and similarily if we multiply U by b:
V•(b*U) = b*(V•U)
so combining these gives:
(a*V)•(b*U) = ab*(V•U)
An example of this type of multiplication is the vector dot product.
However this type of multiplication takes two vectors as input and produces a scalar value as an output. Is it possible to have a bilinear multiplication which takes two vectors as input and produces a vector as an output?
The requirement is:
(a V + a' V')×(b U + b' U') = ab(V×U) + ab'(V×U') +a'b(V'×U) +a'b'(V'×U')
this applies to the vector cross product.
The vector cross product only applies in 1,3 and 7 dimensions. However there are ways to generalise the vector cross product to other numbers of dimensions.
Quadratic Form
If the multiplication is also commutative then the bilinear form is a quadratic form as described on this page.


