Maths - lookAt function

2D lookAt function

How do we calculate the rotation to look at a particular point?

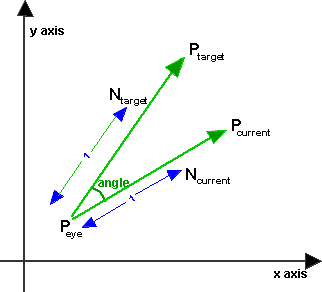
First take the simpler 2D case. We are at P_eye and we are currently looking at P_current what angle do we have to turn to look at P_target?

First we calculate unit length vectors in the current direction and the target direction as follows:

N_current = P_current -P_eye

N_target = P_target -P_eye

The angle between them is then the arcos of dot product of N_current and N_target

3D lookat function

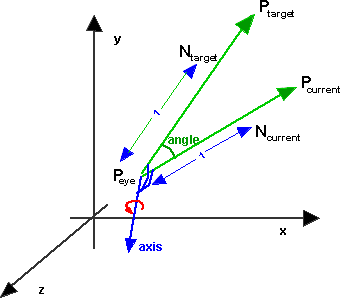
The axis of rotation is a vector which is mutually perpendicular to both P_current and P_target which is given by the cross product of these normalised vectors. The angle is given by arccos of the dot product as described here.

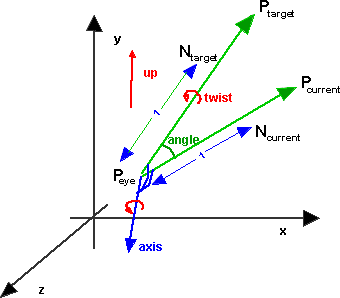
We then need to twist our view around the P_target axis by the angle required to maximise the z component of the up vector. So we now need to apply the following additional rotation:

axis = Ntarget

In order to calculate the angle around Ntarget I think we have to project yaxis and up onto a plane perpendicular to Ntarget. To do that we calculate the projection matrix which is [I] - Ntarget Ntarget^t This is proved here.

So let:

[projection matrix] = [I] - Ntarget Ntarget^t

yaxis' = [projection matrix]yaxis

up' = [projection matrix]up

angle = acos(dot(yaxis',up'))

For discussion of this topic:

• see Open Forum Discussion here
• and minorlogic

The value of 'up' can be a bit arbitrary in some cases, for example, imagine that we want to aim a telescope to look at a given star in the sky: we may only be concerned about getting the star in the centre of the telescope and less concerned about how the other stars are rotated around it. In other words, we may not be concerned about the component of the rotation around the axis between the observer and the target (see box on right for a discussion of the distinction between 'orientation' and 'direction'). Since the direction of the 'up' vector is not important we often use an arbitrary value like (0,1,0) although this is questioned in this thread - here is a quote from it: "Using a constant vector such as (0,1,0), which is the only recommendation I've ran across is no good. You end up rotating the bank axis for no reason, and near singularity points (attitude +-90) the camera spins wildly.  My solution was using [currentRotationMatrix * (0,1,0)] as the up vector. It makes sure only the heading and attitude are changed for the lookAt so the bank is not altered, and it has stood up very well through testing. I highly suggest you mention it on the lookAt page."

Example

Imaging you are in a cuboid room, you on the floor of one corner looking along along the base of one wall, you want to turn to look at the top of the opposite corner. What angle do you have to turn through?

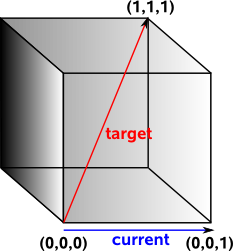
Most people would say that you would need to turn through a heading of 45° and then rotate up at an attitude of 45°. This belief is so strong that programmers will spend days rewriting and debugging their code if they don't get this answer.

In fact we need to turn through a heading of 45° and then rotate up at an attitude of 35°. You turn through 45° and you are now looking at the base of the diagonal corner. You now want to look up to the top of the diagonal side. This forms a triangle where the adjacent side is √2 and the opposite side is 1. So the angle is arctan(0.7071)=35°.

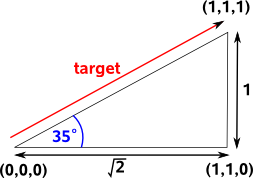
The fallacy here has more to do with the unintuative nature of euler angles than problems with the lookat method but this is a warning not to trust intuition when working with 3D angles and avoid using euler angles whenever possible.

Alternative Method

The components of the vectors of the rotated frame with respect to the un-rotated frame directly give you the rows of the rotation matrix. So the vector Ntarget is one of the three rows of the rotation matrix.

To get the second row, you must specify another property of the orientation by specifying the direction, perpendicular to the forward direction, in which the "up" axis of the object must point.

The third row is the cross product of the other two.

Rotation matrix:

Ntarget

up

Ntarget x up

Can we derive this method from the first method?

First assume the following:

• that up is already projected onto the plane perpendicular to Ntarget
• that eye is at the origin.

The axis of rotation is: Ntarget x Ncurrent

and cos(angle) = Ntarget • Ncurrent

what we need to do is to get the matrix for this rotation, I have been trying to calculate the matrix which gives the rotation between two vectors here but it is getting too complicated can anyone help here?

we also have to project the yaxis onto the plane:

if Ntarget = axis = [a,b,c]

then yaxis' = [-a*b,a*a+c*c,-c*b]

cos(twistAngle) = [up]• [-a*b,a*a+c*c,-c*b] = up.x * (-a*b) + up.y * (a*a+c*c) + up.z * (-c*b)

let,

• cos =cos(twistAngle) = up.x * (-a*b) + up.y * (a*a+c*c) + up.z * (-c*b)
• sin = sin(twistAngle) = sqrt(1-cos*cos)
• t =1 - cos

[twist] =

t*x*x + cos t*x*y - z*sin t*x*z + y*sin t*x*y + z*sin t*y*y + cos t*y*z - x*sin t*x*z - y*sin t*y*z + x*sin t*z*z + cos

again this is getting complicated !

Once we work out these two matricies we need to multiply them to give the the total rotation matrix.

// C++ code
// this code assumes the camera is initially looking towards (1,0,0) positive z direction
// if you want the initial direction to be along the x or y coordinates then try swapping
// the order when setting the components
// dir = target direction
// up = a vector which is perpendicular to the camera axis
void LookAt(const vector3& dir, const vector3& up, matrix33& m) { 
        vector3 z(dir); 
        z.norm(); 
        vector3 x( up * z ); // x = up cross z 
        x.norm(); 
        vector3 y( z * x ); // y = z cross x 
        m.set_components(x,y,z ); 
} 

sfquat LookAt(sfvec3f target,sfvec3f current, sfvec3f eye,sfvec3f up) { 
	// turn vectors into unit vectors 
	n1 = (current - eye).norm();
	n2 = (target - eye).norm();  
	d = sfvec3f.dot(n1,n2); 
	// if no noticable rotation is available return zero rotation
	// this way we avoid Cross product artifacts 
	if( d > 0.9998 ) return new sfquat( 0, 0, 1, 0 ); 
	// in this case there are 2 lines on the same axis 
	if(d < -0.9998){ 
		n1 = n1.Rotx( 0.5f ); 
		// there are an infinite number of normals 
		// in this case. Anyone of these normals will be 
		// a valid rotation (180 degrees). so rotate the curr axis by 0.5 radians this way we get one of these normals 
	} 
	sfvec3f axis = n1;
	axis.cross(n2);
	sfquat pointToTarget= new sfquat(1.0 + d,axis.x,axis.y,axis.z); 
    pointToTarget.norm();
	// now twist around the target vector, so that the 'up' vector points along the z axis
    sfmatrix projectionMatrix=new sfmatrix();
    double a = pointToTarget.x;
    double b = pointToTarget.y;
    double c = pointToTarget.z;
    projectionMatrix.m00 = b*b+c*c;
    projectionMatrix.m01 = -a*b;
    projectionMatrix.m02 = -a*c;
    projectionMatrix.m10 = -b*a;
    projectionMatrix.m11 = a*a+c*c;
    projectionMatrix.m12 = -b*c;
    projectionMatrix.m20 = -c*a;
    projectionMatrix.m21 = -c*b;
    projectionMatrix.m22 = a*a+b*b;
    sfvec3f upProjected = projectionMatrix.transform(up);
    sfvec3f yaxisProjected = projectionMatrix.transform(new sfvec(0,1,0);
    d = sfvec3f.dot(upProjected,yaxisProjected);
    // so the axis of twist is n2 and the angle is arcos(d)
    //convert this to quat as follows   
	double s=Math.sqrt(1.0 - d*d);
	sfquat twist=new sfquat(d,n2*s,n2*s,n2*s);
	return sfquat.mul(pointToTarget,twist);
} 

EuclideanSpace

home

Direction vs. Rotation

Vector Cross Product

Standards