Prerequisites
Vectors can be used to represent direction.
If you are not familiar with this subject you may like to look at the following pages first:
Vector representation of direction
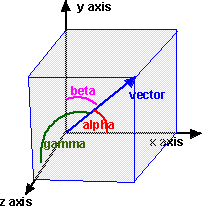
A 3D vector can be used to define a direction. If a vector is used to define direction in this way then the length of the vector is not relevant, therefore we can use a unit length vector.
So if the vector is: (x,y,z)
where:
- x is the length of the vector in the x dimension.
- y is the length of the vector in the y dimension.
- z is the length of the vector in the z dimension.
So for a normalised vector:
x2 + y2 + z2 = 1
The angles from the vector to the coordinate axes are given by:
- x = cos(alpha)
- y = cos(beta)
- z = cos(gamma)
x,y and z are known as the direction cosines.
Distinction between Direction and Orientation
The direction cosines are not independent of each other, they are related by the equation x2 + y2 + z2 = 1, so direction cosines only have two degrees of freedom and can only represent direction and not orientation.
What this means is that direction cosines do not define how much an object is rotated around the axis of the vector.
Further Reading
For applications of unit length vectors to specify direction see here.
You may be interested in means to represent orientation and rotational quantities such as:
Or you may be interested in how these quantities are used to simulate physical objects:

