Axis and Angle is one possible way to represent the rotation of a solid 3D object. Other representations are:
Description
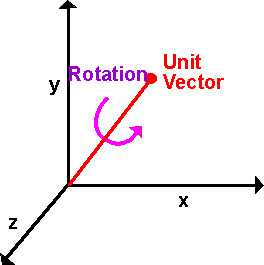
Rotation can be represented by a unit vector and an angle of revolution about that vector.
Any 3D rotation can be represented in this way, in other words, given a solid object with orientation 1 and the same object with a different orientation 2. Then we can always find an axis and angle which will rotate from orientation 1 to orientation 2.
Which direction of rotation is positive? on this site, we will use the right hand rule.
Axis-Angle is probably one of the most easily understood methods for us to specify 3D rotations. However, be careful, 3D rotations can be counterintuitive in some ways (see box on right of page). One downside of using axis angle to represent 3D rotations is that we can't directly combine two rotations to give an equivalent total rotation, to do that we need to use matrices or quaternions, quaternions are related to axis angle so its not too hard convert between them as explained here. The other downside is that there are two singularities at 0° and 180° where the axis can jump suddenly for a small change in input.
We can also use axis and angle to represent any instantaneous angular velocity as explained here.
Generalisation to other numbers of dimensions
Rotation in 1 dimensional space: we cant rotate in one dimension so that does not apply.
Rotation in 2 dimensional space: we only need the angle, the axis is not needed because we only have one plane to rotate in.
Rotation in 3 dimensional space: as covered on the rest of this page.
Rotation in 4 or more dimensional space:
Any rotation can be represented by projecting the object onto a 2-dimentional plane and then rotating it through an angle. The plane can be defined by a bivector .It happens that, in three dimensions, a bivector is three dimensional, in this case planes (represented by bivectors) and lines (represented by vectors) are duals. This means that, in three dimensions, we can represent the direction of rotation by a line known as the axis. This can be helpful as it can be more intuitive to represent the direction of rotation about an axis rather than in a plane.
sfrotation
On these pages will be developing a class sfrotation (full listing here) which holds a rotation and encapsulates operations such as combining two rotations, in addition to coding the rotation as a quaternion it can also be coded as euler or axis angle and can convert between these formats.
Sample Rotations
In order to try to explain things I thought it might help to work out a simple case where rotations are only allowed in multiples of 90°. This should make it easier to illustrate the orientation with a simple aeroplane figure, we can rotate this either about the x,y or z axis as shown here:
Further Reading
You may be interested in other means to represent orientation and rotational quantities such as:
Or you may be interested in how these quantities are used to simulate physical objects:

