
In two dimensions an angle can be a measure of direction or the difference in direction between two lines.
In everyday life we specify angles in degrees. A complete rotation is divided into 360 degrees.
In this program angles are measured in radians where a complete rotation is divided into 2π radians, where π=pi approx 3.14159. Most class libraries such as Java and C# Math libraries use radians, also standards such as VRML. An exception is OpenGL, which uses degrees for some reason.
So to convert from radians to degrees multiply by 180/π =180/3.14159.
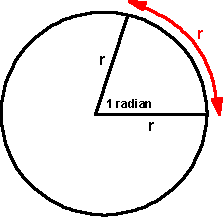
1 radian is given when a distance equal to the radius is measured round the circumference of a circle.
Beyond 360°
When we do a compete rotation of 360° or 2*π radians then we get back to where we started, although this does not imply that the angle jumps back to zero, the angle is continuous everywhere.
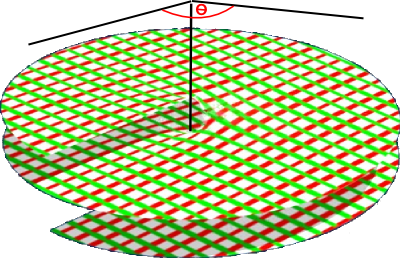
This is illustrated here, this does not imply a third dimension, but it means that we can always find a continuous area to work on (even when we are close to 0° and 360°). This idea is known as a Riemann surface.
We need to be careful about these issues when we look at trig functions and especially their inverses.
Further Reading
You may be interested in other means to represent orientation and rotational quantities such as:

