Maths - Conversion Matrix to Euler

Code

/** this conversion uses conventions as described on page:
*   https://www.euclideanspace.com/maths/geometry/rotations/euler/index.htm
*   Coordinate System: right hand
*   Positive angle: right hand
*   Order of euler angles: heading first, then attitude, then bank
*   matrix row column ordering:
*   [m00 m01 m02]
*   [m10 m11 m12]
*   [m20 m21 m22]*/
public final void rotate(matrix  m) {
    // Assuming the angles are in radians.
	if (m.m10 > 0.998) { // singularity at north pole
		heading = Math.atan2(m.m02,m.m22);
		attitude = Math.PI/2;
		bank = 0;
		return;
	}
	if (m.m10 < -0.998) { // singularity at south pole
		heading = Math.atan2(m.m02,m.m22);
		attitude = -Math.PI/2;
		bank = 0;
		return;
	}
	heading = Math.atan2(-m.m20,m.m00);
	bank = Math.atan2(-m.m12,m.m11);
	attitude = Math.asin(m.m10);
}

Derivation of Equations

This depends on what conventions are used for the Euler Angles. See this page for an explanation of the conventions and standards used on this site.

So it we look at the Euler to Matrix conversion we can see that:

[R] =

ch*ca -ch*sa*cb + sh*sb ch*sa*sb + sh*cb sa ca*cb -ca*sb -sh*ca sh*sa*cb + ch*sb -sh*sa*sb + ch*cb

m20/m00 = -sh / ch = -tan(heading)
m12/m11 = -sb / cb =- tan(bank)
m10 = sa = sin(attitude)

so this gives:

heading = atan2(-m20,m00)
bank = atan2(-m12,m11)
attitude = asin(m10)

I have changed atan(y/x) to atan2(y,x) as described here. Since there are several ways to produce the same rotation using heading, bank and attitude then the solution is not unique. tan(0) is 0, tan(90 degrees) is infinity, tan(-90 degrees) is -infinity. So the results will depend on whether arctan processes a result between -90 and 90 or 0 and 180.

  
atan2(0.0,0.0)=0.0 (although Math.atan2 returns 0 this is abitary and if both    x and y is zero we need to find some other way to get to value)
atan2(0.0,1.0)=0.0
atan2(1.0,1.0)=0.7853981633974483
atan2(1.0,0.0)=1.5707963267948966
atan2(1.0,-1.0)=2.356194490192345
atan2(0.0,-1.0)=3.141592653589793
atan2(-1.0,-1.0)=-2.356194490192345
atan2(-1.0,0.0)=-1.5707963267948966
atan2(-1.0,1.0)=-0.7853981633974483 

This works at all points except the singularities at attitude = +90 and -90 degrees, at these points we will get atan2(0,0) for heading and bank which will return 0 although this is not a vailid result. We therfore need another way to work out heading and bank at the singularities.

Singularity at attitude = +90 degrees = straight up = north pole

ca = 0
sa = 1

which gives

[R] =

0 -ch*cb + sh*sb ch*sb + sh*cb 1 0 0 0 sh*cb + ch*sb -sh*sb + ch*cb

apply trig addition formula:

sin(A+B) = sin A cos B + cos A sin B
cos(A+B) = cos A cos B - sin A sin B

[R] =

0 -c(h+b) s(h+b) 1 0 0 0 s(h+b) c(h+b)

The value we want is has a range of 360 degrees, therefore we need it expressed in atan2 rather than asin or acos, therefore use:

M02/M22 = tan(h+b)

therefore:

h + b = atan2(M02,M22)

in other words, when the aeroplane is flying straight up, it can be rotated by both heading and bank and the rotation is the sum of both. In this case I will choose to use heading and set bank to zero, so,

heading = atan2(M02,M22)
bank = 0

at attitude = -90 degrees

ca = 0
sa = -1

which gives

[R] =

0 ch*cb + sh*sb -ch*sb + sh*cb -1 0 0 0 -sh*cb + ch*sb sh*sb + ch*cb

as before applying trig addition formula:

sin(A-B) = sin A cos B - cos A sin B
cos(A-B) = cos A cos B + sin A sin B

[R] =

0 c(h-b) s(h-b) -1 0 0 0 -s(h-b) c(h-b)

M02/M22 = tan(h-b)

therefore:

h - b = atan2(M02,M22)

in other words, when the aeroplane is flying straight down, it can be rotated by both heading and bank and the rotation is the difference. In this case I will choose to use heading and set bank to zero, so,

heading = atan2(M02,M22)
bank = 0

In order to try to get an intuative understanding of the singularities involved in converting other representations of 3D rotations to Euler angles it may help to look at the way we project the surface of a sphere onto a 2 dimensional map. This is a different case and it only involves two angles, latitude and longitude, but this simpler example may show the principles. This analogy is explained in more detail on this page.

At the north and south poles longitude does not matter so if we are converting some other description of north pole to latitude, longitude it might give any value for longitude, for example, infinity. So we have to be very careful at these points.

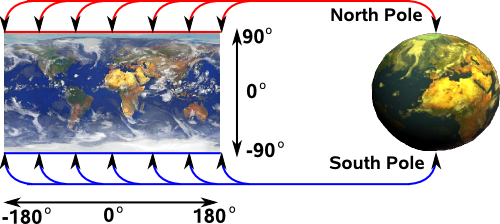
Similarly we can map Euler angles to quaternions (4 dimensional hypersphere). This maps a one dimensional space (rotations around 0,1,0 axis) to a two dimensional plane in Euler terms. This is where attitude = 90° and heading, bank vary:

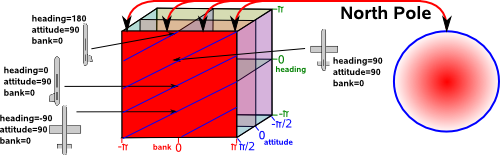
On this plane lines of common orientation are diagonal lines, that is rotation around 0,1,0 axis are given by angle = heading+bank.

Similarly for the south pole.

Example

we take the 90 degree rotation from this:

to this:

As shown here the matrix for this rotation is:

[R] =

1 0 0 0 0 -1 0 1 0

So using the above result:

heading = atan2(-m20,m00) = atan2(0,1) = 0
bank = atan2(-m12,m11) = atan2(1,0) = 90 degrees
attitude = asin(m10) = asin(0) = 0

As you can see here, this gives the result that we are looking for.

We have to be very careful about the following issues:

• One of the intermediate steps involves infinity (division by 0) therefore most maths libraries have an atan2 function to avoid this step.
• Most maths libraries use radians instead of degrees (apart from OpenGL).

Angle Calculator and Further examples

I have put a java applet here which allows the values to be entered and the converted values shown along with a graphical representation of the orientation.

Also further examples in 90 degree steps here