Equations
For a pure rotation, that is where:
Then the matrix can be converted to a quaternion using this basic form:
qw= √(1 + m00 + m11 + m22) /2
qx = (m21 - m12)/( 4 *qw)
qy = (m02 - m20)/( 4 *qw)
qz = (m10 - m01)/( 4 *qw)
But this is only accurate under certain conditions and to get an algorithm that is accurate under all circumstances we need to check the trace as below:
Java Code
Simple Code
public final void set(Matrix4f m1) {
w = Math.sqrt(1.0 + m1.m00 + m1.m11 + m1.m22) / 2.0;
double w4 = (4.0 * w);
x = (m1.m21 - m1.m12) / w4 ;
y = (m1.m02 - m1.m20) / w4 ;
z = (m1.m10 - m1.m01) / w4 ;
}
The above should work assuming that the function inside the square root is positive, that is,
1 + Tr < 0
where Tr = the trace which is the sum of the leading diagonal terms.
For instance the following matrix represents a 180° rotation about the y axis:
In this case the above algorithm wont work because 1 + m00 + m11 + m22 = 0 which gives w=0 and so will cause division by zero.
Another example is a rotation of heading= 180° and attitude = 90°.
Even if the value of qw is very small it may produce big numerical errors when dividing. So it is better to use the following:
1) Calculate the trace(the sum of the diagonal elements) of the matrix T from
the equation:
T = 4 - 4*qx2 - 4*qy2 - 4*qz2
= 4( 1 -qx2 - qy2 - qz2 )
= m00 + m11 + m22 + 1
If the trace of the matrix is greater than zero, then the result is:
S = 0.5 / sqrt(T)
W = 0.25 / S
X = ( m21 - m12 ) * S
Y = ( m02 - m20 ) * S
Z = ( m10 - m01 ) * S
If the trace of the matrix is less than or equal to zero then identify which
major diagonal element has the greatest value.
Code
float tr = m00 + m11 + m22
if (tr > 0) {
float S = sqrt(tr+1.0) * 2; // S=4*qw
qw = 0.25 * S;
qx = (m21 - m12) / S;
qy = (m02 - m20) / S;
qz = (m10 - m01) / S;
} else if ((m00 > m11)&(m00 > m22)) {
float S = sqrt(1.0 + m00 - m11 - m22) * 2; // S=4*qx
qw = (m21 - m12) / S;
qx = 0.25 * S;
qy = (m01 + m10) / S;
qz = (m02 + m20) / S;
} else if (m11 > m22) {
float S = sqrt(1.0 + m11 - m00 - m22) * 2; // S=4*qy
qw = (m02 - m20) / S;
qx = (m01 + m10) / S;
qy = 0.25 * S;
qz = (m12 + m21) / S;
} else {
float S = sqrt(1.0 + m22 - m00 - m11) * 2; // S=4*qz
qw = (m10 - m01) / S;
qx = (m02 + m20) / S;
qy = (m12 + m21) / S;
qz = 0.25 * S;
}
We need to be sure this code is resilient to:
- Avoid division by zero - We need to be sure that S is never zero even with possible floating point errors or de-orthogonalised matrix input.
- Avoid square root of a negative number. - We need to be sure that the tr value chosen is never negative even with possible floating point errors or de-orthogonalised matrix input.
- Accuracy of dividing by (and square rooting) a very small number.
with floating point numbers, dividing small numbers by small numbers
should be reasonably accurate but at the extreme it would loose
accuracy.
- Resilient to a de-orthogonalised matrix
For a discussion of the stability of this code see this forum discussion that I had with Ethan.
Issues
(1) This page assumes that the input matrix represents a pure rotation otherwise the resulting quaternion will not be valid. This implies that the matrix must be special orthogonal, that is both:
If these conditions are satisfied then the resulting quaternion should be normalised (unit length).
(2) Both matrices and quaternions avoid the singularities and discontinuities involved with rotation in 3 dimensions by adding extra dimensions. This has the effect that different values could represent the same rotation, for example quaternion q and -q represent the same rotation. It is therefore possible that, if we are converting a rotation sequence, our output may jump between these equivalent forms. This could cause problems where subsequent operations such as differentiation is done on this data. So programmers need to be aware of this issue.
For a more detailed discussuion of these issues see this forum discussion that I had with Tim.
C++ Code (kindly sent to me by Angel)
There is also code from minorlogic at the end of this page.
This includes code for both normalised and unnormalised quaternions.
inline void CalculateRotation( Quaternion& q ) const {
float trace = a[0][0] + a[1][1] + a[2][2]; // I removed + 1.0f; see discussion with Ethan
if( trace > 0 ) {// I changed M_EPSILON to 0
float s = 0.5f / sqrtf(trace+ 1.0f);
q.w = 0.25f / s;
q.x = ( a[2][1] - a[1][2] ) * s;
q.y = ( a[0][2] - a[2][0] ) * s;
q.z = ( a[1][0] - a[0][1] ) * s;
} else {
if ( a[0][0] > a[1][1] && a[0][0] > a[2][2] ) {
float s = 2.0f * sqrtf( 1.0f + a[0][0] - a[1][1] - a[2][2]);
q.w = (a[2][1] - a[1][2] ) / s;
q.x = 0.25f * s;
q.y = (a[0][1] + a[1][0] ) / s;
q.z = (a[0][2] + a[2][0] ) / s;
} else if (a[1][1] > a[2][2]) {
float s = 2.0f * sqrtf( 1.0f + a[1][1] - a[0][0] - a[2][2]);
q.w = (a[0][2] - a[2][0] ) / s;
q.x = (a[0][1] + a[1][0] ) / s;
q.y = 0.25f * s;
q.z = (a[1][2] + a[2][1] ) / s;
} else {
float s = 2.0f * sqrtf( 1.0f + a[2][2] - a[0][0] - a[1][1] );
q.w = (a[1][0] - a[0][1] ) / s;
q.x = (a[0][2] + a[2][0] ) / s;
q.y = (a[1][2] + a[2][1] ) / s;
q.z = 0.25f * s;
}
}
}
Alternative Method
Christian has suggested an alternative algorithm and he makes a convincing argument that this is more efficient here.
There is a potential issue with the use of 'copysign' as described here.
quaternion.w = sqrt( max( 0, 1 + m00 + m11
+ m22 ) ) / 2;
quaternion.x = sqrt( max( 0, 1 + m00 - m11
- m22 ) ) / 2;
quaternion.y = sqrt( max( 0, 1 - m00 + m11
- m22 ) ) / 2;
quaternion.z = sqrt( max( 0, 1 - m00 - m11
+ m22 ) ) / 2;
Q.x = _copysign( Q.x, m21 - m12 )
Q.y = _copysign( Q.y, m02 - m20 )
Q.z = _copysign( Q.z, m10 - m01 )
- The max( 0, ... ) is just a
safeguard against rounding error.
- copysign takes the sign from the second term and sets the sign of the first without altering the magnitude, I don't know of a java equivalent.
Scaling
Since it is possible for both matrices and quaternions to represent scaling in addition to rotation, then it would be possible to include this in the convertion. In most cases this is not necessary, as we only want to represent rotations, but if you do need to include a scale factor then you might want to try this method suggested by Christian.
Of course, this will mean that the matrix is no longer orthogonal and that the quaternion is no longer normalised.
We first calculate absQ2 which is the cube root of the volume
spanned by the matrix axes.
absQ2 = det(
matrix )^(1/3)
quaternion.w = sqrt( max( 0,
absQ2 + m00 + m11 + m22 ) ) / 2;
...etc
Rounding Errors
When comparing different methods
of doing this conversion I think we should consider sensitivity to rounding errors. In other words, the matrix
contains redundant information so, althrough a matrix may initially be orthogonal, if we then do some rotation operations rounding errors may
de-orthogonalise the matrix, if this happens which method is most
likely to cancel out the errors?
I don't know
how best to tackle this? say, for instance, rounding errors
introduce an error 'delta e' to one element of
the matrix, but we don't know which element has the error. Which
method is most likely to cancel out this error? Which method is
most likely to produce a normalised
quaternion?
Derivation of Equations
Quaternion multiplication and orthogonal matrix multiplication can both be
used to represent rotation. If a quaternion is represented by qw + i
qx + j qy + k qz , then the equivalent matrix, to represent the
same rotation, is:
| 1 - 2*qy2 - 2*qz2 |
2*qx*qy - 2*qz*qw |
2*qx*qz + 2*qy*qw |
| 2*qx*qy + 2*qz*qw |
1 - 2*qx2 - 2*qz2 |
2*qy*qz - 2*qx*qw |
| 2*qx*qz - 2*qy*qw |
2*qy*qz + 2*qx*qw |
1 - 2*qx2 - 2*qy2 |
This assumes that the quaternion is normalised (qw2 + qx2
+ qy2 + qz2 =1) and that the matrix is orthogonal.
This
page discusses the equivalence of quaternion multiplication and orthogonal
matrix multiplication.
So this gives the following equations:
- m00 = 1 - 2*qy2 - 2*qz2
- m01 = 2*qx*qy - 2*qz*qw
- m02 = 2*qx*qz + 2*qy*qw
- m10 = 2*qx*qy + 2*qz*qw
- m11 = 1 - 2*qx2 - 2*qz2
- m12 = 2*qy*qz - 2*qx*qw
- m20 = 2*qx*qz - 2*qy*qw
- m21 = 2*qy*qz + 2*qx*qw
- m22 = 1 - 2*qx2 - 2*qy2
This contains more information than we need, so we need to choose a method
which is less sensitive to matrix not being orthogonal.
If the quaternion is normalised: qx2 + qy2 + qz2+
qw2 = 1
so,
qw2 = 1 - qx2 - qy2 - qz2
multiply both sides by 4 gives,
4 * qw2 = 4 - 4*qx2 - 4*qy2 - 4*qz2
4 * qw2 = 1 + 1 - 2*qy2 - 2*qz2 + 1 - 2*qx2
- 2*qz2 + 1 - 2*qx2 - 2*qy2
4 * qw2 = 1 + m00 + m11 + m22
so qw= ±½√(1 + m00 + m11 + m22)
the sum of the diagonal elements is known as the trace (Tr), this gives,
qw= sqrt (1 + Tr) /2
this method can only be used if we are taking the square root of a positive
number ie,
1 + Tr <= 0
Is this always the case for orthogonal
matrices ???
So we have an equation for qw, to get the other values we can use:
m21 - m12 = 2*qy*qz - 2*qx*qw - 2*qy*qz - 2*qx*qw
m21 - m12 = 4 *qx*qw
therefore:
qx = (m21 - m12)/( 4 *qw)
now calculate qy
m02 - m20 = 2*qx*qz + 2*qy*qw - 2*qx*qz + 2*qy*qw
m02 - m20 = 4*qy*qw
therefore:
qy = (m02 - m20)/( 4 *qw)
now calculate qz,
m10 - m01 = 2*qx*qy + 2*qz*qw - 2*qx*qy + 2*qz*qw
m10 - m01 = 4*qz*qw
therefore:
qz = (m10 - m01)/( 4 *qw)
so summarising the results:
- qw= ±½√(1 + m00 + m11 + m22)
- qx = (m21 - m12)/( 4 *qw)
- qy = (m02 - m20)/( 4 *qw)
- qz = (m10 - m01)/( 4 *qw)
Different Methods
There are 4 related methods to calculate the conversion. This gives us alternatives to calculate the result when the simple method above would require us to calculate the square root of a negative number. We can calculate either of the quaternion terms (qw, qx, qy or qz) from the leading diagonal terms of the matrix and then calculate the other terms from the non-diagonal terms:
| m00=1 - 2*qy2 - 2*qz2 |
m01=2*qx*qy - 2*qz*qw |
m02=2*qx*qz + 2*qy*qw |
| m10=2*qx*qy + 2*qz*qw |
m11=1 - 2*qx2 - 2*qz2 |
m12=2*qy*qz - 2*qx*qw |
| m20=2*qx*qz - 2*qy*qw |
m21=2*qy*qz + 2*qx*qw |
m22=1 - 2*qx2 - 2*qy2 |
By adding and subtracting these terms we can separate out the quaternion terms.
From the diagonal terms:
- qw=±½√(1 + m00 + m11 + m22)
- qx=±½√(1 + m00 - m11 - m22)
- qy=±½√(1 + m11 - m00 - m22)
- qz=±½√(1 + m22 - m00 - m11)
From the non diagonal terms (subtracting terms):
- qx*qw = ¼(m21-m12)
- qy*qw = ¼(m02-m20)
- qz*qw = ¼(m10-m01)
From the non diagonal terms (adding terms):
- qy*qz = ¼(m21+m12)
- qx*qz = ¼(m02+m20)
- qx*qy = ¼(m10+m01)
combining these diagonal and non-diagonal results we get:
| method 1 (qw from diagonal) |
method 2 (qx from diagonal) |
method 3 (qy from diagonal) |
method 4 (qz from diagonal) |
|
qw=±½√(1 + m00 + m11 + m22) |
qx*qw = ¼(m21-m12)
gives:
qw = (m21-m12)/(4*qx) |
qy*qw = ¼(m02-m20)
gives:
qw = (m02-m20)/(4*qy) |
qz*qw = ¼(m10-m01)
gives:
qw = (m10-m01)/(4*qz) |
m21 - m12 = 2*qy*qz - 2*qx*qw - 2*qy*qz - 2*qx*qw
m21 - m12 = 4 *qx*qw
therefore:
qx = (m21 - m12)/( 4 *qw) |
1 + m00 - m11 - m22
= 1 + 1 - 2*qy² - 2*qz² - 1 + 2*qx² +
2*qz² - 1 + 2*qx² + 2*qy²
= 4*qx²
therefore:
qx=±½√(1 + m00 - m11 - m22) |
qx*qy = ¼(m10+m01)
gives:
qx = (m10+m01)/(4*qy) |
qx*qz = ¼(m02+m20)
gives:
qx = (m02+m20)/(4*qz) |
m02 - m20 = 2*qx*qz + 2*qy*qw - 2*qx*qz + 2*qy*qw
m02 - m20 = 4*qy*qw
therefore:
qy = (m02 - m20)/( 4 *qw) |
qx*qy = ¼(m10+m01)
gives:
qy = (m10+m01)/(4*qx) |
1 + m11 - m00 - m22
= 1 + 1 - 2*qx² - 2*qz² - 1 + 2*qy² +
2*qz² - 1 + 2*qx² + 2*qy²
= 4*qy²
therefore:
qy=±½√(1 + m11 - m00 - m22) |
qy*qz = ¼(m21+m12)
gives:
qy = (m21+m12)/(4*qz) |
m10 - m01 = 2*qx*qy + 2*qz*qw - 2*qx*qy + 2*qz*qw
m10 - m01 = 4*qz*qw
therefore:
qz = (m10 - m01)/( 4 *qw) |
qx*qz = ¼(m02+m20)
gives:
qz = (m02+m20)/(4*qx) |
qy*qz = ¼(m21+m12)
gives:
qz = (m21+m12)/(4*qy) |
1 + m22 - m00 - m11
= 1 +1 - 2*qx² - 2*qy² - 1 + 2*qy² +
2*qz² - 1 + 2*qx² + 2*qz²
= 4*qz²
therefore:
qz=±½√(1 + m22 - m00 - m11) |
So, in theory, we can calculate the quaternion from just the diagonal terms. This would require us to calculate 4 square roots, there is a problem with this, the result of a square root may be either positive or negative and therefore we can't determine the signs of the terms. It is therefore better to calculate one quaternion term from the diagonal and the remaining terms from the non-diagonal. We still have to choose the sign of this first term, we can choose either positive or negative because there are two possible quaternions that can represent any given 3D rotation, what matters is the relative signs of the terms.
Another issue is the speed of the calculation, the square root function has always been taken to be slow, this may be less so on modern computers. I must admit, I have not tested it, but even so I think its best to minimise the number of square roots.
Perhaps the most important issue is the accuracy of the result, if the value derived from the diagonal is small, then any errors in this value will be multiplied up when we calculate the other values. Therefore we may get the most accurate result if we choose the column in the table above which not only avoids the square root of a negative number but also gives the largest diagonal term for the particular rotation that we are calculating.
Rotation about a point other than origin
Quaternions and 3×3 matrices alone can only represent rotations about the origin.
But if we include a 3D vector with the quaternion we can use this to represent
the point about which we are rotating. Also if we use a 4×4 matrix then this
can hold a translation (as explained
here) and therefore can specify a rotation about a point.
The following code generates a 3D vector (representing the centre of rotation)
from the 4x4 matrix. The theory is given
here.
|
|
= 1/det[m] * |
| (m11 - 1)*m22 - m12*m21 |
m02*m21 - m01*(m22 - 1) |
m01*m12 - m02*(m11 - 1) |
| m12*m20 - m10*(m22 - 1) |
m00*(m22 - 1) - m02*m20 |
m02*m10 - (m00 - 1)*m12 |
| m10*m21 - (m11 - 1)*m20 |
m01*m20 - (m00 - 1)*m21 |
m00*(m11 - 1) - m01*m10 |
|
|
Example
| we take the 90 degree rotation from this: |
 |
to this: |
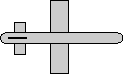 |
As shown here
the matrix for this rotation is:
So using the above result:
qw= sqrt (1 + m00 + m11 + m22) /2 = sqrt (2)/2 = 1.4142/2 = 0.7071
qx = (m21 - m12)/( 4 *qw) = 2/(4 * 0.7071) = 1/ 1.4142 = 0.7071
qy = (m02 - m20)/( 4 *qw) = 0
qz = (m10 - m01)/( 4 *qw) = 0
This gives the quaternion 0.7071 + i 0.7071
As you can see here,
this gives the result that we are looking for.
Angle Calculator and Further examples
I have put a java applet here which allows the values to be entered and the converted values shown along with a graphical representation of the orientation.
Also further examples in 90 degree steps here
Here is a simple javascript calculator, input matrix values then press calculate button:
This site may have errors. Don't use for critical systems.

