Kinematics: The study and description of motion, without regard to its causes, for example, we can calculate the end point of a robot arm from the angles of all its joints. Alternatively, given the end point of the robot arm, we could calculate the angles and settings of all its joints required to put it there (inverse kinematics - IK). Kinematics can be studied without regard to mass or physical quantities that depend on mass.
We will talk about dynamics later. One way to think about the difference between kinematics and dynamics is that dynamics is the cause of motion and kinematics is the effect.
Kinematics involves position, velocity and acceleration (and their rotational equivalents).
- Position is the point in space that an object occupies, this needs to be defined in some coordinate system.
- Velocity is the rate of change of position with respect to time.
- Acceleration is the rate of change of velocity with respect to time.
Although I am leaving the dynamics to later it is worth mentioning here that, if there are no net forces acting on an object, then it will have a constant velocity. Also if there is a constant net force acting on an object, like gravity for instance, then it will have constant acceleration. So these special cases of constant velocity and of constant acceleration are worth considering in more detail.
Movement in one dimension
If an object is moving in a straight line, and if we measure its position along that line, then its position, velocity and acceleration can all be represented by scalar quantities. This makes the analysis much easier, so lets start there.
Constant Velocity (no net force)
Velocity is the rate if change of position:
v = dp/dt
| where: | |||
symbol |
description |
type |
units |
| v | velocity | vector | m/s |
| p | position, distance from a given point | vector | m |
| t | time | scalar | s |
| d ... /dt | rate of change | ||
So integrating both sides gives:
p = ∫v dt
so if v is constant:
p = p0 + v t
| where: | |||
symbol |
description |
type |
units |
| v | velocity | vector | m/s |
| p | position, distance from a given point | vector | m |
| t | time | scalar | s |
| p0 | position at time t=0 | vector | m |
Constant Acceleration (constant force)
Velocity is the rate if change of position:
a = dv/dt
So integrating both sides gives:
v = ∫a dt
so if a is constant:
v = v0 + a*t
| where: | |||
symbol |
description |
type |
units |
| v | velocity | vector | m/s |
| a | acceleration (dv/dt) | vector | m |
| t | time | scalar | s |
| v0 or u | velocity at time t=0 (sometimes written u) | vector | m/s |
So integrating acceleration once gives the velocity, to get the position we need to integrate again:
p = ∫v dt
p = ∫(v0 + a*t) dt
p = p0 + v0 t + ½ a t2
Variable Acceleration - approximate methods
If we have an equation for the acceleration, as a function of time, we can apply integration to find the velocity and position, if we don't then we can use approximate methods such as finite difference method, Eulers Method or Runge-Kutta Method. If we are animating a computer simulation then this can be a very good method because we need to generate the position for each frame anyway, so is is much easier to generate the next frame from the frame before it.
vn+1 = vn + a * dt
| where: | |||
symbol |
description |
type |
units |
| vn+1 | velocity at frame n+1 | vector | m/s |
| vn | velocity at frame n | vector | m/s |
| a | acceleration | vector | m/s2 |
| dt | time between frame n and frame n+1 | scalar | s |
and summing again:
pn+1 = pn + vn * dt
| where: | |||
symbol |
description |
type |
units |
| pn+1 | position at frame n+1 | vector | m/s |
| pn | position at frame n | vector | m/s |
| vn | velocity at frame n | vector | m/s |
| dt | time between frame n and frame n+1 | scalar | s |
These approximations can be made more accurate by using Eulers Method or Runge-Kutta Method
Position in three dimensions (Location and Orientation)
When we are working in 3 dimensions the scalar quantities in the 1D case p,
v and a need to be replaced by 3D vectors, ![]() ,
,
![]() and
and ![]() .
Also in order to define the position of an object in 3 dimensions we need to
know both its location and its orientation. This gives it a maximum of 6 degrees
of freedom (6DOF) 3 for linear movement, 3 for rotation.
.
Also in order to define the position of an object in 3 dimensions we need to
know both its location and its orientation. This gives it a maximum of 6 degrees
of freedom (6DOF) 3 for linear movement, 3 for rotation.
So the following state vector defines the position completely using 6 scalar quantities.
| θx |
| θy |
| θz |
| Px |
| Py |
| Pz |
Note: this has mixed units, the top 3 are radians, the bottom 3 are metres.
If an object is constrained, for instance it may be linked to other objects by a hinge, or other types of join, then it may have less than 6 degrees of freedom.
It can be useful to represent the location and orientation as a single vector, specially when we get onto acceleration and dynamics equations, it is not so useful for position because we cant use vector addition to represent rotation. I have included it here to start introducing the Featherstone's spatial vector notation (see http://www.syseng.anu.edu.au/~roy/technical.html) Thank you to Michael Shantz telling me about this (see hybridgdc.pdf file at http://michaelshantz.com ).
When we define the position of a solid object we need to do this relative to some point on the object, also this is the point that the object rotates around. So we need to define a local coordinate system on the body. If we take the planetary motion example then, in the case of the earth, we could choose to measure relative to the middle of the earths core, or a place on the surface, or any other location. Now as the earth is moving, both the translation and orientation are functions of time.
If we choose to measure the local coordinate system relative to a point on the surface, then the translation will be a complicated function of time, but if we measure the local coordinate system relative to the centre of the earth then the translation will be a less complicated function of time. So in this case it is better, but not necessary, to have a local coordinate system relative to the centre of the earth. The orientation as a function of time is independent of the local reference point, in the case of the earth, one rotation per day.
Transforms
Matrices can be used to perform various operations on objects such as translation, rotation, scaling and sheer. When we representing solid objects, then we want to limit our transforms to translations and rotations only, so a 4x4 matrix contains redundant information and we have to be careful not to do any other operations on it.
Complex jointed objects, for example a robot arm, can be represented on a hierarchy of transform groups, see here for more details.
In theory we could specify our translation/rotation with a single 6 dimensional vector, however as explained under rotation, this is not as useful as it might seem as multiple transforms can't be represented by simple arithmetic operations on the vectors.
| θx |
| θy |
| θz |
| Px |
| Py |
| Pz |
Note: this has mixed units, the top 3 are radians, the bottom 3 are metres.
Multiple transforms can only be represented by adding their vectors, if the transforms are infinitesimally small. This means that 6 dimensional vectors are useful for combining velocities and accelerations.
Uniform Angular Speed
Although vector addition cannot be used for angles, it does begin to approximate the correct value as the angle gets smaller, for infinitesimal rotations vector algebra can be used therefore vector algebra can be used to combine rotations. A rotation vector [w] contains 3 values rotation about x, rotation about y and rotation about z.
6d Velocity vector
It may be useful to have a single state vector which can represent the angular and linear velocities. So that operations on this velocity can be represented by a single equation which includes both the linear and rotational effects.
| wx |
| wy |
| wz |
| Vx |
| Vy |
| Vz |
Note: this has mixed units, the top 3 are radians/sec, the bottom 3 are metres/sec.
For example if an object were moving within a frame-of-reference and the frame-of-reference itself were moving, we could calculate the vector representing the absolute velocity by adding together the vectors representing the velocity of the frame-of-reference and the relative velocity. However we have to be very careful here, it works OK for the linear component (provided we are using Newtonian relativity and not Einsteinian relativity), but for the rotational part we must be careful if the rotations are not about the same point, in this case the movement could be some complex spiral or planetary motion, but the addition may still work for instantaneous values.
Uniform Angular Acceleration
The angular acceleration vector is the rate of change of angular velocity.6D acceleration vector
A single state vector representing both the angular and linear acceleration. This can be very useful in dynamics (see here), for instance, this single equation relates the torques, forces and acceleration of an object.
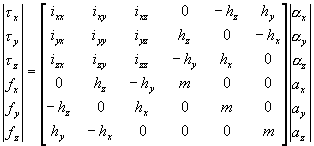
Simulation by the program
I have defined a suggested kinematics node to represent the kinematics behavior because VRML and Java3D don't yet have such a node.
These equations for uniform acceleration can be solved analytically to give:
- v = v0 + a*t
- p = p0 + v0 t + ½ a t2
- v2 = v02 + 2 * a * p
where v0 = initial velocity and s = delta x (i.e. distance moved)
However in a realtime simulation it is faster to do the integration numerically, this is done by the program in the kinematicsBean, the algorithm to do this is explained here.