Here we investigate how to transform between different frames of reference (different observers) which may be moving relative to each other at a constant velocity.
There is no way, by doing physics experiments that we can determine an absolute velocity, these things always have to be measured relative to something. This relativity principle applies both to Newtonian and Einsteinian physics although, as we will see below, the nature of the velocity transform depends on which of these we are using.
The Galilean transform can be represented by a shear matrix, the Lorentz transform is a hyperbolic rotation.
Galilean transform
Lets start with the Galilean transform which assumes the classical Newtonian laws of physics, that is we ignore the anomalies that come from Maxwell's equations, the speed of light, etc.
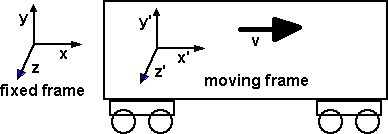
Assuming the relative motion 'vx' is along the x dimension then x'=x-vt so the transform will be:
|
= |
|
|
Lorentz transform
The Lorentz transform relates the spacetime coordinates (t,x,y,z) to (t',x',y',z'), spacetime in different frames.
Assuming the relative motion 'vx' is along the x dimension then the transform will be:
|
= |
|
|
where:
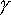= 1/√(1 - ß2) - b = ß/√(1 - ß2)
- ß = v/c
- v = relative velocity
- c = speed of light
We can represent this as an hyperbolic rotation
|
= |
|
|
where:
- φ = rapidity (phi symbol)
Comparing the two forms gives:
b = ß
is replaced by
v cosh(φ) = c sinh(φ)
or
tanh(φ)=v/c
The rapidity (φ) is useful for composition of velocities, that is: if we know the velocity of frame A relative to frame B and we know the velocity of frame B relative to frame C what is we know the velocity of frame A relative to frame C?
There are two ways that we can do this:
- We can multiply the Lorentz transforms to give the combined Lorentz transform.
- We can add the rapidity angles.
Addition of rapidity angles can be derived from the trig identity:
tanh(A+B) = (tanh A + tanh B)/(1 + tanh A tanh B)
from this page.
At small velicities the rapidity approximates to the velocity, that is special relativity approximates to classical mechanics, this is because the tanh function passes through the origin with a slope of 1.
Generalising to hyperbolic rotation in 3 dimensions
If the velocity is not along the 'x' dimension then we can rotate in the3 space dimensions, apply the simple Lorentz transform, then apply the reverse space rotation.
|
= |
|
|
|
|
Any 4x4 matrix (or corresponding linear transformation) that preserves the quadratic form xt G x is called Lorentz.
Lorentz matrices constitutes a group under matrix multiplication.
