Maths - Trigonometry

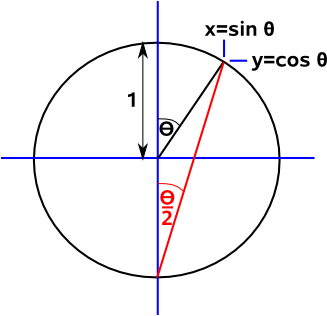
Applications

These functions are very useful in geometry of course. However they are widely used in mathematics, physics and engineering.

Right Angle Triangle

The sine, cosine and tangent functions represent how the ratio of the sides of a right angled triangle varies with the angle. These can be defined by a right angled triangle in two dimensions as follows:

Let:

  • a = the length of the edge opposite the right angle
  • b = the length of the edge opposite the angle
  • c = the length of the edge adjacent to the angle
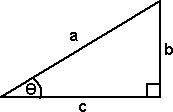 triangle

The ratio of these lengths depends on the angle θ and we can define the following functions for each of the ratios:

sine function sin(θ) = b / a  
cosine function cos(θ) = c / a  
tangent function tan(θ) = b / c  
cosecant cosec(θ) = a / b  
secant sec(θ) = a / c  
cotangent cot(θ) = c / b  

these functions are related to each other as follows:

tan(θ) = sin(θ) / cos(θ)

cosec(θ) = 1 / sin(θ)

sec(θ) = 1 / cos(θ)

cot(θ) = 1 / tan(θ)

Terminology and Notation

The angle

The angle being considered is usually denoted by the greek letter theta: θ.

We can also denote the angle by three points which define that angle, for example in the above diagram:

θ = ABC

Where the middle point is where the angle is measured between the other two points.

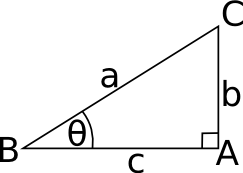 triangle

The sides

The sides can be denoted in different ways:

hypotenuse - the side opposite the right angle a BC
opposite - the side opposite the angle being considered b AC
adjacent - the side adjacent to the angle being considered c AB

The Vertices

The points of the triangle, the vertices, are here denoted by upper case letters A,B and C

The Trig Functions

The main trigometric functions are: sine, cosine and tangent. These are often abbreviated to sin, cos and tan.

There are three others cosecant, secant and cotangent . They not used so often because they are the reciprocal of sine, cosine and tangent. They are abbreviated to cosec, sec and cot.

Trig Identities

The values of sin, cos and tan are related to each other, for instance,

These 'identities' can be proved by using the sides of a right angled triangle as follows:

tan A = b / c = (b / a) / (c / a) = sin A/cos A

From Pythagoras we know:

b2 + c2 = a2

dividing both sides by a2 gives:

b2 / a2 + c2 / a2 = 1

cos2A + sin2A = 1

Complimentary and Supplementary Angles

Two angles whose sum is 90° are said to be complimentary, each is said to be the compliment of the other. Where the sum is 180° the angles are said to be supplementary.

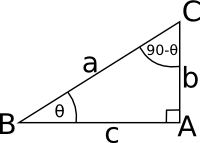triangle

sin(θ - 90°) = BA / BC = cos(θ)

cos(θ - 90°) = AC / BC = sin(θ)

tan(θ - 90°) = AC / AB = cot(θ)

Non-Right Angled Triangles - The Sine Rule

We started with right angled triangles but we can also use trig functions for other triangles:

Acute angled triangle

Drop a perpendicular from A to BC and let AD = h, then,

sin B = h / c

h = c sin B

similarly,

sin C = h / b

h = b sin C

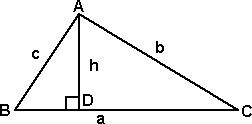acute angled triangle

combining these gives:

c sin B = b sin C

so,

b / sin B = c / sin C

similarly if we put a perpendicular from B onto AC we can show that:

a / sin A = c / sin C

So, combining these, we get:

a / sin A = b / sin B = c / sin C

where:

Obtuse angled triangle

This time we need to extend the line from B to C onto D so that it can meet a perpendicular from A.

sin B = h / c

h = c sin B

similarly,

sin ACD = h / b

h = b sin ACD

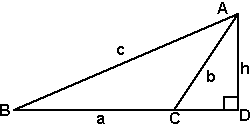acute angled triangle

combining these gives:

c sin B = b sin ACD

but sin ACD = sin(180° - ACD) = sin c

so,

b / sin B = c / sin C

similarly if we put a perpendicular from B onto AC we can show that:

a / sin A = c / sin C

So, combining these, we get:

a / sin A = b / sin B = c / sin C

where:

Example 1

solve triangle ABC if:

Angles of triangle add up to 180° so,

B = 180° - (70° + 58°16')

B = 51°74'

since: a / sin A = b / sin B then,

a = b * sin A/ sin B

a = 6m * sin 70°/ sin 51°74'

a = 6.63m

Example 2

solve triangle ABC if:

b / sin B = c / sin C

sin C = sin B * c / b

C = 51°44'

however this is an ambiguous case since there is also a solution at sin(180°-51°19')

Non-Right Angled Triangles - The Cosine Rule

We can use this to solve for triangles where the sine rule is not applicable (when we know 2 sides and the included angle).

We create a perpendicular to the side b, mark the point this joins as D.

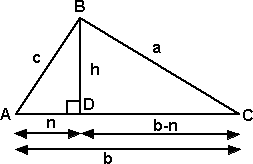cosine rule

We can apply Pythagoras to the two inner triangles:

h2 = c2 - n2

a2 = (b-n)2 - h2

expanding the second one, and substitute the first for h, gives:

a2 = b2 - 2bn + n2+ c2 - n2

a2 = b2 - 2bn + c2 but n = c cos A which gives,

a2 = b2 + c2 - 2*b*c*cos A

we can do similar constructions based on the other sides:

b2 = c 2 + a 2 - 2*c*a*cos B

c2 = a 2 + b 2 - 2*a*b*cos C

rearranging these equations gives:

cos A = (b2 + c2 - a2)/2*b*c

cos B = (c2 + a 2 - b 2)/2*c*a

cos C = (a2 + b 2 - c 2)/2*a*b

Area of triangles

The area of a triangle is: 1/2 base * perpendicular height

therefore:

area = 1/2 a * h

but h = c*sin B therefore,

area = 1/2 a * c*sin B

 acute angled triangle

similarly we can do the same construction for the other sides:

area = 1/2 a * b*sin C

area = 1/2 b * c*sin A

This is half the product of two sides and the sin of the included angle.

Addition Formulae

We want to express sin(A+B) in terms of trig ratios

sin(A+B)

From the diagram we can see that the area of the whole is equal to the sum of the areas of the inner triangles:

area LMP = area LMN + area LNP

0.5 p m sin(A+B) = 0.5 n p sin A + 0.5 m n sin B

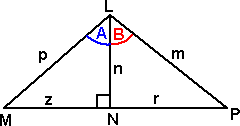 addition formulae

which gives:

sin(A+B) = (n/m) sin A + (n/p) sin B

but n/m = cos B and n/p = cos A

substituting these gives:

sin(A+B) = sin A cos B + cos A sin B

cos(A+B)

apply cos rule:

cos(A+B) = (p2 + m2 - (q+r)2)/2*m*p

cos(A+B) = (p2 + m2 - q2- 2*q*r- r2)/2*m*p

cos(A+B) = ((p2 - q2)+(m2 - r2)- 2*q*r) / 2*m*p

cos(A+B) = (n2+n2- 2*q*r) / 2*m*p

cos(A+B) = (n2- q*r) / m*p

cos(A+B) = n2/m*p - q*r/m*p

cos(A+B) = n/p * n/m - q/p * r/m

cos(A+B) = cos A cos B - sin A sin B

tan(A+B)

tan(A+B) = sin(A+B)/cos(A+B)

tan(A+B) = (sin A cos B + cos A sin B)/(cos A cos B - sin A sin B)

divide top & bottom by cos A cos B

tan(A+B) = ((sin A cos B/cos A cos B) + (cos A sin B/cos A cos B))/((cos A cos B/cos A cos B) - (sin A sin B/cos A cos B))

tan(A+B) = ((sin A /cos A) + (sin B/cos B))/(1 - (sin A sin B/cos A cos B))

tan(A+B) = (tan A + tan B)/(1 - tan A tan B)

Double Angle Formulae

from addition formulae if A=B

The second form of the cos(2A) formula can be proved as follows:

from the addition formulae if A=B we get:

cos(2A) = cos2A - sin2A

but we can combine this with the identity:

cos2A + sin2A = 1

substituting

cos(2A) = (1 - sin2A) - sin2A

cos(2A) = 1 - 2*sin2A

I have put further information about double angle and half angle formulae on the page here.

Subtraction formulae

from addition formulae if A=B

Angles of Any Magnitude

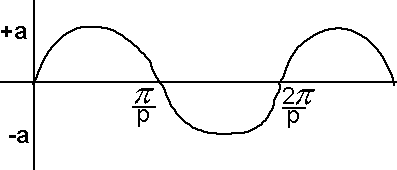
So far we have defined the trig functions using right angled triangles and therefore used angles between 0 and 90 degrees however we can extend the concept of sine, cosine, etc. and use angles beyond that range. If we plot the angle (theta) across (left to right) and the ratio of sides up (bottom to top) then we get a wave-like function like this which repeats continuously in both directions:

sine wave

Angle Sign

If theta is formed by OP rotating about O and rotation is anticlockwise theta is said to be positive. If clockwise theta is said to be negative.

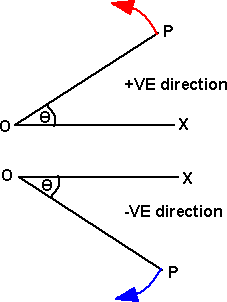
angle sign

Results

Because the trig functions repeat like this, we can derive the values outside 0°-90° from the values inside the 0°-90° range.

Quadrants

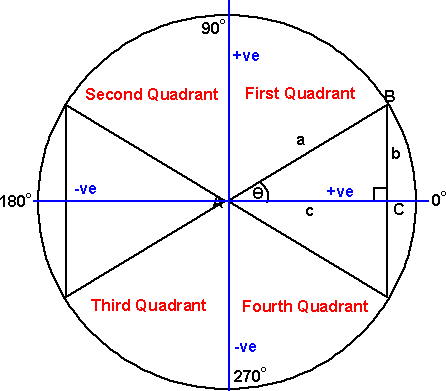
quadrants of triange

First Quadrant

In the first quadrant, angles between 0° and 90°, both the x axis and the y axis are positive, therefore the ratios are positive, and all the trig functions are positive.

Second Quadrant

In the second quadrant, angles between 90 ° and 180°, the x axis is negative and the y axis is positive, therefore:

sine function sin(θ) = b(+ve) / a(+ve) = (+ve)  
cosine function cos(θ) = c(-ve) / a(+ve) = (-ve)  
tangent function tan(θ) = b(+ve) / c(-ve) = (-ve)  
cosecant cosec(θ) = a(+ve) / b(+ve) = (+ve)  
secant sec(θ) = a(+ve) / c(-ve) = (-ve)  
cotangent cot(θ) = c(-ve) / b(+ve) = (-ve)  

Third Quadrant

In the first quadrant, angles between 180° and 270°, both the x axis and the y axis are negative, therefore:

sine function sin(θ) = b(-ve) / a(+ve) = (-ve)  
cosine function cos(θ) = c(-ve) / a(+ve) = (-ve)  
tangent function tan(θ) = b(-ve) / c(-ve) = (+ve)  
cosecant cosec(θ) = a(+ve) / b(-ve) = (-ve)  
secant sec(θ) = a(+ve) / c(-ve) = (-ve)  
cotangent cot(θ) = c(-ve) / b(-ve) = (+ve)  

Fourth Quadrant

In the second quadrant, angles between 270 ° and 360°, the x axis is negative and the y axis is positive, therefore:

sine function sin(θ) = b(-ve) / a(+ve) = (-ve)  
cosine function cos(θ) = c(+ve) / a(+ve) = (+ve)  
tangent function tan(θ) = b(-ve) / c(+ve) = (-ve)  
cosecant cosec(θ) = a(+ve) / b(-ve) = (-ve)  
secant sec(θ) = a(+ve) / c(+ve) = (+ve)  
cotangent cot(θ) = c(+ve) / b(-ve) = (-ve)  
metadata block
see also:

 
Correspondence about this page

Book Shop - Further reading.

Where I can, I have put links to Amazon for books that are relevant to the subject, click on the appropriate country flag to get more details of the book or to buy it from them.

cover Mathematics for 3D game Programming - Includes introduction to Vectors, Matrices, Transforms and Trigonometry. (But no euler angles or quaternions). Also includes ray tracing and some linear & rotational physics also collision detection (but not collision response).

Other Math Books

This site may have errors. Don't use for critical systems.

Copyright (c) 1998-2023 Martin John Baker - All rights reserved - privacy policy.