Maths - Trigonometry

Periodic functions of the type y = a sin px

The graph of y = a sin(px) is similar to that of the sin graph of y = sin(x). Instead of varying or oscillating between +1 and -1, a sin(px) will vary between +a and -a. 'a' is called the amplitude and affects only the scale for y. The graph will repeat itself when the angle px increases by 360° or 2π radians. i.e. when x increases by 360°/p or 2π/p radians thus the period is 2π/p radians.

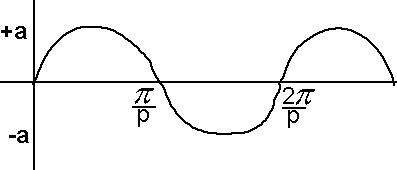
Thus 5 sin(2x) has a period of 2π/2 = π radians and amplitude 5. Hence there are 2 waves between 0° and 360°.

Example

Sketch the curve for y = 3 sin(x+60°)

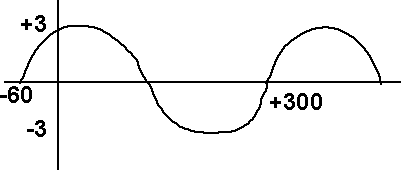
y = 3 sin(x+60°) is said to have a phase lead of 60° since its values are those of y = 3 sin(x) with x increased by 60°. y = 3 sin(x-60°) is said to lag by 60°.

Solving Trig Equations

Here are some suggestions for solving trig identities:

1. Change secant, cosecant and cotan into cos, sin and tan.
2. rewrite in terms of sin and cos (use tan = sin/cos)
3. If in second degree (ie cos² or sin²) look for posible cos²A + sin²A = 1 relationship.
4. If it contains cos² or sin² change sin² into cos²-1 and solve resulting quadratic.
5. If all this fails convert to an infinite series.
6. If this fails plot as a graph.

Plotting trig functions

Example 1

y = 3 sin(2x) + sin x

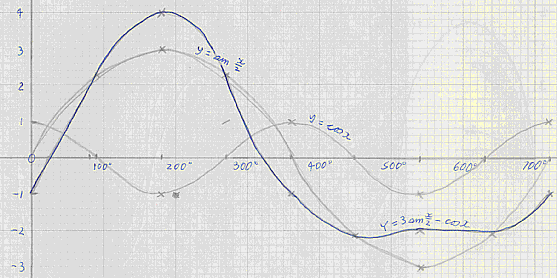
Example 2

y = 3 sin(x/2) - cos x

Prerequisites

This page assumes you know how angles are measured, using degrees or radians, in a two dimensional plane. If not see:

• Angles

Elements of Equations

Problem Solving