Physics - Velocity as a Rotation in Space-Time

Overview

This page investigates velocities in moving frames of reference. We investigate whether ideas from relativity can be used in classical Euclidean space.

Velocity as a Rotation in Space-Time

In relativity space and time is treated as a combined 4 dimensional space instead of separate 3 and 1 dimensional spaces. Here we stay with classical physics but try to use the space-time idea. Just to be clear: we are using conventional Euclidean space and are not using and concepts like the constant speed of light.

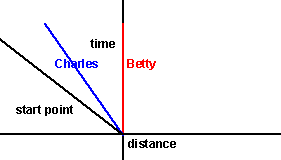
So imagine that Betty and Charles start walking at different speeds from the same point in time and space. Their positions can be plotted in space and time by a stationary person (Adam) and the plot may look like this:

The equations for these lines are:

x = v_bt for Betty and
x = v_ct for Charles

where:

• v_b= velocity of Betty
• v_c= velocity of Charles

What if we want to measure these things in the frame of reference of say Charles? then we would get:

Since Charles does not move relative to himself then his line will be vertical (along the time axis). We get these graphs by subtracting v_bt from the distance axis, which gives:

x = v_bt - v_ct = (v_b- v_c)t for Betty and
x = v_ct - v_ct = 0 for Charles
x = -v_ct for absolute values such as the start point

So the axes are skewed relative to the absolute frame of reference.

For completeness here is the space-time diagram relative to Betty:

giving the equations:

x = v_bt - v_bt = 0 for Betty and
x = v_ct - v_bt = (v_c- v_b)t for Charles
x = -v_bt for absolute values such as the start point.

Representing as a Rotation

Is it possible, instead of skewing the distance axis, to skew the time axis or rotate the axes?

tan(θ)=x/t ?

Transform due to Relative Velocity

If we want to transform an event measured in two reference frames one of which is traveling at velocity v compared with the other we could use:

x -> x₀ + vt

where:

• v = relative velocity of the two reference frames.

which would look like this:

—»

in other words point:

t x

is transformed to:

t x + vt

Galilean Transforms

Galilean Transforms give a transform from on inertial frame to another in classical Newtonian physics.

EuclideanSpace

home