I think of orientation as the current angular position of an object and rotation as an operation which takes a starting orientation and turns it into a possibly different orientation. However both rotation and orientation can be defined in the same way, provided we have a reference orientation we can always define orientation as a rotation from its reference orientation.
When dealing with a solid object, it may not be symmetrical, so we may need to know which way round it is.
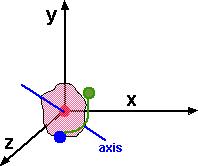
One possible way to define this might be as follows, imagine the earth is transparent and you are at the centre of it (imagining that the world revolves around you may be easier for some people than for others), you can then specify a direction to face by giving its latitude and longitude. However there is also another direction that you can rotate, if you are looking at a particular point in space, you can rotate to see it upside down, or any angle in-between. In other words you can rotate about the line between yourself and the point you are looking at. I'm not sure what this angle is measured from, where is zero? can anyone help me? perhaps where (0,1,0) in local coordinates translates to the maximum value in absolute coordinates?
There are many other ways to specify orientation, but all of them require 3 or more real numbers. Using this method the orientation might be specified by the following vector:
| θlatitude |
| θlongitude |
| θaxis |
A related way to specify the orientation would be to replace the latitude and longitude with a unit vector, this gives the axis and angle notation as follows:
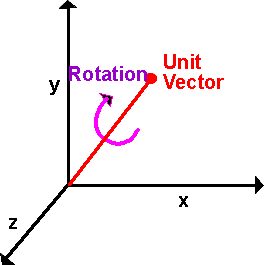
This requires 4 real numbers to specify, to remove the redundant information we normalise the vector to make it unit length.
| x |
| y |
| z |
| θ |
Another related way to specify orientation is quaternion algebra. This differs from axis-angle in that the real value is cos (θ/2) and the imaginary values are the unit vector divided by sin(θ/2).
| real = cos (θ/2) |
| imaginary i = x / sin(θ/2) |
| imaginary j = y / sin(θ/2) |
| imaginary k = z / sin(θ/2) |
Another way to specify orientation is to start with the object that has not been rotated, in other words the objects local x,y and z coordinates are in the same directions as the absolute x,y and z coordinates, then apply rotations about each axis in turn.
This can be represented by 3 floating point or double floating point numbers to contain angles representing rotation about the x,y and z axes.
| θx |
| θy |
| θz |
Since rotation is not commutative the result depends on the order that we apply the rotations about each axis (more info).
LookAt function
Information here about how to orientate object to point towards a particular point.
Representing Orientation in program
Orientation in 3D space can be held in a quaternion (see class sfrotation) or a matrix (see class sftransform). For an example of how this might be used in a scenegraph node, see here.
Position of particle on solid object
If we have a particle of a solid object and we want to measure its position when the object is in a given orientation. In two dimensions the position would be given by:
p = [r sin θ, r cos θ]
In three dimensions it we could start by using cylindrical coordinates and then convert these to Cartesian coordinates:
So,
|
= |
|
where:
- Px,Py,Pz = Cartesian coordinates of particle (absolute coordinates).
- Ax, Ay, Az = unit length vector giving direction of arbitrary axis which object is rotating around.
- r = distance of particle from arbitrary axis.
- h = distance of particle along arbitrary axis.