Prerequisites
If you are not familiar with this subject you may like to look at the following pages first:
Position Vector
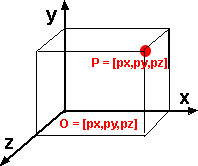
We need a coordinate system to represent the position of an object. I have explained Cartesian and Polar coordinate systems here. The maths here is much easier if we use Cartesian co-ordinates, for 3 dimensions the position of any point (P) can be represented by 3 real (floating point or double floating point) numbers. This is usually represented as a vector of dimension 3:
| Px |
| Py |
| Pz |
where the 3 numbers represent the position in each of the, usually perpendicular, directions in an arbitrary reference frame. These Cartesian coordinates are usually called x (left & right), y (up and down), z (back and forward). On this site we are using a right handed coordinate system as described here.
Representing position in program
Position in 3D space can be held in a 3D vector (see class sfvec3f). For an example of how this might be used in a scenegraph node, see here.
Position of particle on solid object
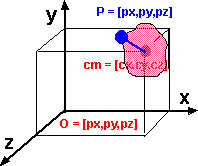
If we have a particle of a solid object and we want to measure its position, then:
p = cm + r
| where: | |||
symbol |
description |
type |
units |
| cm | position of centre of mass of object | vector | m |
| r | position of particle relative to object | vector | m |
| p | position of particle in absolute coordinates | vector | m |