A normal is a unit vector which is perpendicular to
the surface. It is often used in rendering 3D scenes to calculate now the light
sources are reflected to the camera view. So the normals are often included
in the scene graph to speed up rendering. For more about using unit length vectors
to specify direction see
here.
Note: In OpenGL etc. normals are only used for lighting, back face culling
is done using the winding order of the coordinates.
Calculation of normals from mesh data
The normals can be calculated from Indexed Face Set coordinates as follows:
- Calculate the normal to each face.
- If you require a normal per vertex (without crease angle), calculate this
by adding the normals for each face adjoining the vertex, and then normalising.
Calculate the normal to each face.
Conventions
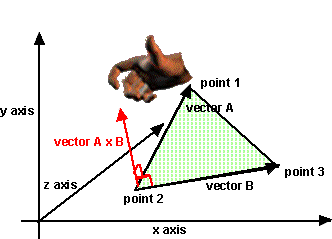
- The vector points outward from the object, i.e. the object will be seen
from the side the vector points toward.
- The points are assumed to be ordered the same way round for all faces (known
as the winding order) which allows the normal direction to be determined.
- This order is given by the right hand rule, i.e. if the fingers of the right
hand curl in the direction given by point1, point2, point3... then the thumb
will point in the direction of the normal.
- The conventions for the coordinates are shown here.
Method 1 - Using cross product.
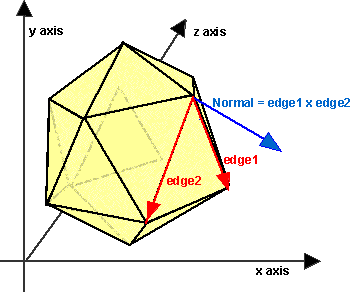
This can be calculated by taking the cross product
of any 2 of its edges, and then normalising. We need to be careful to check
the following conditions:
- The two edges chosen must not be parallel, i.e. the angle between the edges
must not be 0 or 180 degrees. The normal will be more accurate if the angle
between the lines is closer to 90 degrees.
- The length of the edges must be non-zero and the normal will be more accurate
if the length is high compared with the accuracy of the coordinates.
- If the angle is concave then the direction of the normal needs to be reversed.
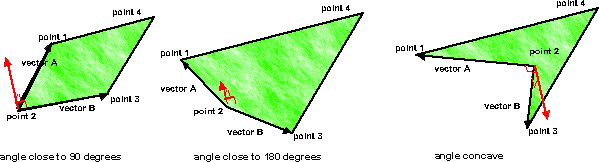
These conditions are more likely to be met if the edges chosen are adjacent
to each other, i.e. if they share a common point then they are less likely to
be parallel to each other.
In order to avoid a concave angle, then this common point should be further
away from the centre than the other points.
Java code to generate a normal to the whole face:
sfvec3f generateFaceNormal(sfvec3f a,sfvec3f b,sfvec3f c){
sfvec3f v1 = sfvec3f.sub(a,b);
sfvec3f v2 = sfvec3f.sub(a,c);
v1.cross(v2);
v1.normalize();
return v1;
}
Managed C++code to generate a normal to the whole face:
sfvec3f* triangleHolder::generateFaceNormal(sfvec3f* a,sfvec3f* b,sfvec3f* c){
sfvec3f* v1 = sfvec3f::sub(a,b);
sfvec3f* v2 = sfvec3f::sub(a,c);
v1->cross(v2);
v1->normalize();
return v1;
}
Method 2 - using the area projections.
If the above conditions are likely to cause problems then there is a more complex
method which uses all the points:
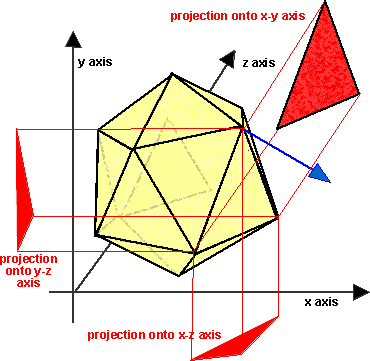
Calculate the area of the polygon when projected onto the y-z, x-z and x-y
axes.
This is equivalent to a sum of triangle normal vectors formed by all edges
of the polygon with respect to some reference point in the plane such as the
centroid of all vertices.
Per vertex Normal
We can now calculate this by adding the normals for each face adjoining the
vertex, and then normalising.
creaseAngle
The creaseAngle field, used by the ElevationGrid, Extrusion, and IndexedFaceSet
nodes, affects how default normals are generated. If the angle between the geometric
normals of two adjacent faces is less than the crease angle, normals shall be
calculated so that the faces are smooth-shaded across the edge; otherwise, normals
shall be calculated so that a lighting discontinuity across the edge is produced.
For example, a crease angle of 0.5 radians means that an edge between two adjacent
polygonal faces will be smooth shaded if the geometric normals of the two faces
form an angle that is less than 0.5 radians. Otherwise, the faces will appear
faceted. Crease angles shall be greater than or equal to 0.0.
Managed C++ code
I don't claim this code is very good so please send me improvements.
void triangleHolder::generateNormals(double creaseAngle){
if (normals) normals->clear();
else normals = new mfvec3f();
int vertexPerFace =3;
if (primitive== triangleHolder::prim::QUAD_ARRAY) vertexPerFace =4;
for (int i=0;i<coordinates->howmany();i=i+vertexPerFace) {
sfvec3f* a=coordinates->getEntry(i);
sfvec3f* b=coordinates->getEntry(i+1);
sfvec3f* c=coordinates->getEntry(i+2);
sfvec3f* sfv=generateFaceNormal(a,b,c);
normals->setEntry(sfv,i);
normals->setEntry(sfv,i+1);
normals->setEntry(sfv,i+2);
if (vertexPerFace>3) normals->setEntry(sfv,i+3);
}
if (creaseAngle < 0.9) { // average out normals for identical points
mfint32* coordInd = new mfint32(); // build an array which shows the first index
// where a coordinate occurs
for (int i=0;i<coordinates->howmany();i++) {
sfvec3f* a=coordinates->getEntry(i);
int index = coordinates->findIndex(a);
if (index < 0) index = i;
coordInd->addEntry(index);
}
for (int j=0;j<coordInd->howmany();j++) {
int k=coordInd->getValue(j);
if (k==j) { // this is the first occurance of this coordinate
// so we need to find the others and average out their normals
// find number of coordinates with this value
int n=1;
for (int m=k+1;m<coordInd->howmany();m++) {
if (k==coordInd->getValue(m)) n++;
}
if (n>1) { // if there are more than 1 average out their normals
sfvec3f* averagedNorm=new sfvec3f(normals->getEntry(k));
for (int m=k+1;m<coordInd->howmany();m++) {
if (k==coordInd->getValue(m)) {
averagedNorm->add(normals->getEntry(m));
}
}
averagedNorm->normalize();
for (int m=0;m<coordInd->howmany();m++) { // put avaraged values back in norms
if (k==coordInd->getValue(m)) {
normals->setEntry(averagedNorm,m);
}
}
}
}
}
}
This site may have errors. Don't use for critical systems.






