Maths - Rays

A ray specifies a start point and a direction from the point. So to define it requires two 3D vectors. A 3D vector to reperesent the start point and a normalised (unit length) 3D vector to represent its direction.

mjbWorld uses rays for picking, i.e. when the mouse is pressed working out which object to select.

how to generate ray

Once this ray has been generated we need to traverse through the scenegraph to find, which objects intersect with the ray, and which of those objects are closest to start of the ray (ie the viewpoint).

The following sections show how to determine if each type of node intersects with the ray and then calculate the distance of the node from the start of the ray.

In addition to the geometry nodes, we also need to consider the result of putting the geometry nodes inside a Transform node. So for each of these nodes we need to define a function which returns -1 if the ray does not intersect with the node, and otherwise a positive number representing the distance from the start of the ray to the node.

Sphere Node

We need to have a method to determine if a ray, if extended, would pass through a sphere. This method is required for the picking routines in the program.

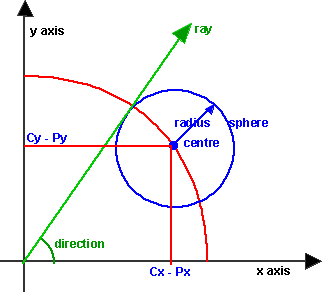
In the following assume all coordinates are measured relative to the start point of the ray (ie the viewpoint/camera position). If you want to use absolute coordinates the replace Cx, Cy, Cz with (Cx - Px), (Cy - Py), (Cz - Pz) and Dx, Dy, Dz with (Dx - Px), (Dy - Py), (Dz - Pz) where Px, Py, Pz is the start point of the ray.

The distance from P (start of ray) to the centre of the sphere is:

sqrt(Cx*Cx + Cy*Cy + Cz*Cz)

 

The ray, by definition, has unit length, so it we multiply it by the above value it will be long enought to reach the sphere (if it is pointing in the right direction). So if the original ray end point is:

| Dx |
| Dy |
| Dz |

Then when multiplied up the new end point is:

| Vx | = Dx * sqrt(Cx*Cx + Cy*Cy + Cz*Cz)
| Vy | = Dy * sqrt(Cx*Cx + Cy*Cy + Cz*Cz)
| Vz | = Dz * sqrt(Cx*Cx + Cy*Cy + Cz*Cz)

So the ray will pass through the sphere if V is inside the sphere.

The distance of V from C is:

sqrt( (Cx-Vx)^2 + (Cy-Vy)^2 + (Cy-Vy)^2)

if this is greater than R (the radius of the sphere) then the ray does not pass through the sphere, so the test for intersection is:

R > sqrt( (Cx-Vx)^2 + (Cy-Vy)^2 + (Cy-Vy)^2)

Before we do this test, it is best to check whether, the start point is already inside the sphere (in which case the ray must intersect) and then if the ray is pointing away from the sphere (in which case ray cannot intersect). So the test is as follows:

if (R > sqrt( (Cx)^2 + (Cy)^2 + (Cy)^2) return 0 // the start point is already inside the sphere so the distance to it is zero
if (sqrt( (Cx-Vx)^2 + (Cy-Vy)^2 + (Cy-Vy)^2) > sqrt( Cx^2 + Cy^2 + Cy^2)) return -1 // the distance of the centre is greater than the distance to the beginning so its pointing away
if (R < sqrt( (Cx-Vx)^2 + (Cy-Vy)^2 + (Cy-Vy)^2) return -1 // The distance of V from C is greater than R so its outside
return sqrt(Cx*Cx + Cy*Cy + Cz*Cz) - R // return distance to the nearest point

The code for java is as follows:

void intersection(sfvec3f rayStart,sfvec3f rayDirection,sfnode nearestNode,sfvec3f distance) {
	sfvec3f c = getSphereCentre().clone();
	c.sub(rayStart); // c=centre of sphere relative to start of ray
	double r = getSphereRadius(); // r=radius of sphere
	double distanceToSphere = Math::sqrt((c.x * c.x) + (c.y * c.y) + (c.z * c.z));
	if (r> distanceToSphere) { // the start point is already inside the sphere so the distance to it is zero
		nearestNode.setNode(this);
        distance.set(0.0);
		return; 
	}
	double vx = rayDirection.x * distanceToSphere;
	double vy = rayDirection.y * distanceToSphere;
    double vz = rayDirection.z * distanceToSphere; // v = end point of ray when projected to sphere orbit
	double distanceFromEnd=Math::sqrt(((c.x - vx)*(c.x - vx)) + ((c.y - vy)*(c.y - vy)) + ((c.z - vz)*(c.z - vz)));
	if (distanceFromEnd > distanceToSphere) return; // the distance of the centre is greater than the distance to the beginning so its pointing away
	if (R < distanceFromEnd) return; // The distance of V from C is greater than R so its outside
	double d=distance.getValue();
	if ((d < 0.0) | (d > distanceToSphere - R)) {
    	distance.set(distanceToSphere - R); // return distance to the nearest point
		nearestNode.setNode(this);
	}
}

The code for managed C++ is as follows:

void sphereBean::intersection(sfvec3f* rayStart,sfvec3f* rayDirection,sfnode* nearestNode,sfvec3f* distance) {
	sfvec3f* c = getSphereCentre()->clone();
	c->sub(rayStart); // c=centre of sphere relative to start of ray
	double r = getSphereRadius(); // r=radius of sphere
	double distanceToSphere = Math::Sqrt((c->x * c->x) + (c->y * c->y) + (c->z * c->z));
	if (r> distanceToSphere) { // the start point is already inside the sphere so the distance to it is zero
		nearestNode->setNode(this);
        distance->set(0.0);
		return; 
	}
	double vx = rayDirection->x * distanceToSphere;
	double vy = rayDirection->y * distanceToSphere;
    double vz = rayDirection->z * distanceToSphere; // v = end point of ray when projected to sphere orbit
	double distanceFromEnd=Math::Sqrt(((c->x - vx)*(c->x - vx)) + ((c->y - vy)*(c->y - vy)) + ((c->z - vz)*(c->z - vz)));
	if (distanceFromEnd > distanceToSphere) return; // the distance of the centre is greater than the distance to the beginning so its pointing away
	if (R < distanceFromEnd) return; // The distance of V from C is greater than R so its outside
	double d=distance->getValue();
	if ((d < 0.0) | (d > distanceToSphere - R)) {
    	distance->set(distanceToSphere - R); // return distance to the nearest point
		nearestNode->setNode(this);
	}
}

Box Node

We need to have a method to determine if a ray, if extended, would pass through a box. This method is required for the picking routines in the program.

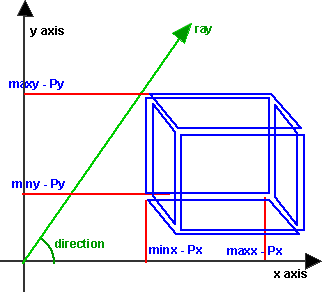
The method is to seperately test if the ray passes through each of the faces of the box.

So, for each face, we extend the ray to the plane that the face is in, and then test if the intersection point is inside the minimum and maximum dimeantions of the box.

For the face at x==minx ,then we extend the ray to make Vx = minx, to keep the ray pointing in the same direction we also have to multiply its other coodinates by the same factor (minx / Dx).

| Vx | = Dx * minx / Dx = minx
| Vy | = Dy * minx / Dx
| Vz | = Dz * minx / Dx

so if

(Dy * minx / Dx < maxy) & (Dy * minx / Dx > miny) & (Dz * minx / Dx < maxz) & (Dz * minx / Dx > minz)

then the ray intersects with this face. So the following is the test for intersection with all 6 faces:

((Dy * minx / Dx < maxy) & (Dy * minx / Dx > miny) & (Dz * minx / Dx < maxz) & (Dz * minx / Dx > minz)) |
((Dy * maxx / Dx < maxy) & (Dy * maxx / Dx > miny) & (Dz * maxx / Dx < maxz) & (Dz * maxx / Dx > minz)) |
((Dx * miny / Dy< maxx) & (Dx * miny / Dy> minx) & (Dz * miny / Dy< maxz) & (Dz * miny / Dy> minz)) |
((Dx * maxy / Dy< maxx) & (Dx * maxy / Dy> minx) & (Dz * maxy / Dy< maxz) & (Dz * maxy / Dy> minz)) |
((Dx * minz / Dz< maxx) & (Dx * minz / Dz> minx) & (Dy * minz / Dz< maxy) & (Dy * minz / Dz> miny)) |
((Dx * maxz / Dz< maxx) & (Dx * maxz / Dz> minx) & (Dy * maxz / Dz< maxy) & (Dy * maxz / Dz> miny))

As in the sphere example we first need to check if the ray starts inside the box, and also if the ray is pointing away from the box.

So the full code is:

The code for java is as follows:

void intersection(sfvec3f rayStart,sfvec3f rayDirection,sfnode nearestNode,sfvec3f distance) {
	double xmin = getWidth()/2 - rayStart.x;
	double xmax = getWidth()/2 - rayStart.x;
	double ymin = getHeight()/2 - rayStart.y;
	double ymax = getHeight()/2 - rayStart.y;
	double zmin = getDebth()/2 - rayStart.z;
	double zmax = getDebth()/2 - rayStart.z;
	if ((Dx < maxx) & (Dx > minx) & (Dy < maxy) & (Dy > miny) & (Dz < maxz) & (Dz > minz)) { // the start point is already inside the sphere so the distance to it is zero
		nearestNode.setNode(this);
        distance.set(0.0);
		return; 
	}
	double boxCentroidx = (xmax + xmin)/2;
	double boxCentroidy = (ymax + ymin)/2;
	double boxCentroidz = (zmax + zmin)/2;
	double distanceToCentroid = Math::Sqrt(boxCentroidx*boxCentroidx + boxCentroidy*boxCentroidy + boxCentroidz*boxCentroidz);
	double vx = rayDirection.x * distanceToCentroid;
	double vy = rayDirection.y * distanceToCentroid;
    double vz = rayDirection.z * distanceToCentroid; // v = end point of ray when projected to box orbit
	double distanceFromEnd=Math::sqrt(((boxCentroidx - vx)*(boxCentroidx - vx)) + ((boxCentroidy - vy)*(boxCentroidy - vy)) + ((boxCentroidz - vz)*(boxCentroidz - vz)));
	if (distanceFromEnd > distanceToCentroid) return; // the distance of the centre is greater than the distance to the beginning so its pointing away
	if (((Dy * minx / Dx < maxy) & (Dy * minx / Dx > miny) & (Dz * minx / Dx < maxz) & (Dz * minx / Dx > minz)) |
        ((Dy * maxx / Dx < maxy) & (Dy * maxx / Dx > miny) & (Dz * maxx / Dx < maxz) & (Dz * maxx / Dx > minz)) |
        ((Dx * miny / Dy < maxx) & (Dx * miny / Dy > minx) & (Dz * miny / Dy < maxz) & (Dz * miny / Dy > minz)) |
        ((Dx * maxy / Dy < maxx) & (Dx * maxy / Dy > minx) & (Dz * maxy / Dy < maxz) & (Dz * maxy / Dy > minz)) |
        ((Dx * minz / Dz < maxx) & (Dx * minz / Dz > minx) & (Dy * minz / Dz < maxy) & (Dy * minz / Dz > miny)) |
        ((Dx * maxz / Dz < maxx) & (Dx * maxz / Dz > minx) & (Dy * maxz / Dz < maxy) & (Dy * maxz / Dz > miny))) return -1.0; // The distance of V from C is greater than R so its outside
	double d=distance.getValue();
	if ((d < 0.0) | (d > distanceToCentroid)) {
    	distance.set(distanceToCentroid); // I really want to return distance to the nearest point not the centrod is there a way to do this
		nearestNode.setNode(this);
	}
}

The code for managed C++ is as follows:

void boxBean::intersection(sfvec3f* rayStart,sfvec3f* rayDirection,sfnode* nearestNode,sfvec3f* distance) {
	double xmin = getWidth()/2 - rayStart->x;
	double xmax = getWidth()/2 - rayStart->x;
	double ymin = getHeight()/2 - rayStart->y;
	double ymax = getHeight()/2 - rayStart->y;
	double zmin = getDebth()/2 - rayStart->z;
	double zmax = getDebth()/2 - rayStart->z;
	if ((Dx < maxx) & (Dx > minx) & (Dy < maxy) & (Dy > miny) & (Dz < maxz) & (Dz > minz)) { // the start point is already inside the sphere so the distance to it is zero
		nearestNode->setNode(this);
        distance->set(0.0);
		return; 
	}
	double boxCentroidx = (xmax + xmin)/2;
	double boxCentroidy = (ymax + ymin)/2;
	double boxCentroidz = (zmax + zmin)/2;
	double distanceToCentroid = Math::Sqrt(boxCentroidx*boxCentroidx + boxCentroidy*boxCentroidy + boxCentroidz*boxCentroidz);
	double vx = rayDirection->x * distanceToCentroid;
	double vy = rayDirection->y * distanceToCentroid;
    double vz = rayDirection->z * distanceToCentroid; // v = end point of ray when projected to box orbit
	double distanceFromEnd=Math::Sqrt(((boxCentroidx - vx)*(boxCentroidx - vx)) + ((boxCentroidy - vy)*(boxCentroidy - vy)) + ((boxCentroidz - vz)*(boxCentroidz - vz)));
	if (distanceFromEnd > distanceToCentroid) return; // the distance of the centre is greater than the distance to the beginning so its pointing away
	if (((Dy * minx / Dx < maxy) & (Dy * minx / Dx > miny) & (Dz * minx / Dx < maxz) & (Dz * minx / Dx > minz)) |
        ((Dy * maxx / Dx < maxy) & (Dy * maxx / Dx > miny) & (Dz * maxx / Dx < maxz) & (Dz * maxx / Dx > minz)) |
        ((Dx * miny / Dy < maxx) & (Dx * miny / Dy > minx) & (Dz * miny / Dy < maxz) & (Dz * miny / Dy > minz)) |
        ((Dx * maxy / Dy < maxx) & (Dx * maxy / Dy > minx) & (Dz * maxy / Dy < maxz) & (Dz * maxy / Dy > minz)) |
        ((Dx * minz / Dz < maxx) & (Dx * minz / Dz > minx) & (Dy * minz / Dz < maxy) & (Dy * minz / Dz > miny)) |
        ((Dx * maxz / Dz < maxx) & (Dx * maxz / Dz > minx) & (Dy * maxz / Dz < maxy) & (Dy * maxz / Dz > miny))) return; // The distance of V from C is greater than R so its outside
	double d=distance->getValue();
	if ((d < 0.0) | (d > distanceToCentroid)) {
    	distance->set(distanceToCentroid); // I really want to return distance to the nearest point not the centrod is there a way to do this
		nearestNode->setNode(this);
	}
}

Indexed Face Set Node

Can anyone help me with this?

Cylinder Node

Can anyone help me with this?

Cone Node

Can anyone help me with this?

Text Node

Can anyone help me with this?

Extrusion Node

Can anyone help me with this?

Elivationgrid Node

Can anyone help me with this?

Indexed Line Set Node

Can anyone help me with this?

Transform

We are traversing the scenegraph to find the objects which intersect the ray. When we are transversing below a transform node, it is not very efficient to transform all the nodes under the transform nodes just for this test. It is more efficient to work in the local coordinates of the subnodes and instead to transform the start and direction of the ray. The following is to work out how to translate the ray:

Translation:

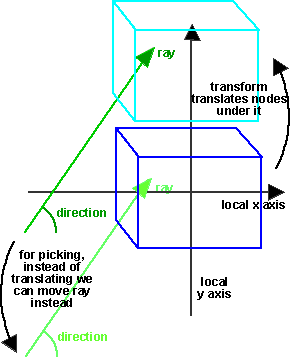
So under a Transform which is translated by (x,y,z) the equivalent ray is transformed by:

Start Point: transform = (-x,-y,-z)

Direction: transform = (0,0,0)

Rotation:

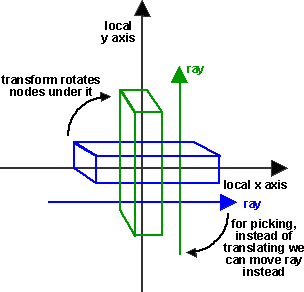
So under a Transform which is rotated by (x,y,z,angle) the equivalent ray is transformed by:

Start Point: rotation = (x,y,z,-angle)

Direction: rotation = (x,y,z,-angle)

Scale:

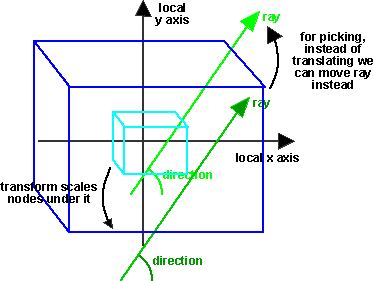
For scaling we need to scale the start point by the inverse factor, if the scaling factor is the same in all directions then there is no need to alter the direction, but if the scaling factors are different then we need to scale by the inverse factor and then normalise.

So under a Transform which is scaled by (x,y,z) the equivalent ray is transformed by:

Start Point: scale = (1/x,1/y,1/z)

Direction: scale = normalise(1/x,1/y,1/z)

Overall transform:

So the following gives the

The code for java is as follows:

void boxBean::intersection(sfvec3f rayStart,sfvec3f rayDirection,sfnode nearestNode,sfvec3f distance) {
    sftransform transform = new sftransform();
    transform.calcTransform(getTranslation(),getRotation(0),
                          getCenter(0),getScale(0),getScaleOrientation(0));
	transform.invert();
	sfvec3f localStart = new sfvec3f(rayStart);
	transform.transform(localStart);
	transform.m03 = 0.0;
	transform.m13 = 0.0;
	transform.m23 = 0.0;
	sfvec3f localDirection = new sfvec3f(rayDirection);
	transform.transform(localDirection);
	for (int i=0;i<subnodes.get_Count();i++) {
		nodeBean sgo = (nodeBean)(subnodes.get_Item(i));
		sgo.intersection(localStart,localDirection,nearestNode,distance);
	}
}

The code for managed C++ is as follows:

void transformGroupBean::intersection(sfvec3f* rayStart,sfvec3f* rayDirection,sfnode* nearestNode,sfvec3f* distance) {
    sftransform* transform = new sftransform();
    transform->calcTransform(getTranslation(),getRotation(0),
                          getCenter(0),getScale(0),getScaleOrientation(0));
	transform->invert();
	sfvec3f* localStart = new sfvec3f(rayStart);
	transform->transform(localStart);
	transform->m03 = 0.0;
	transform->m13 = 0.0;
	transform->m23 = 0.0;
	sfvec3f* localDirection = new sfvec3f(rayDirection);
	transform->transform(localDirection);
	for (int i=0;i<subnodes->get_Count();i++) {
		nodeBean* sgo = dynamic_cast<nodeBean*>(subnodes->get_Item(i));
		sgo->intersection(localStart,localDirection,nearestNode,distance);
	}
}
metadata block
see also:

 
Correspondence about this page

Book Shop - Further reading.

Where I can, I have put links to Amazon for books that are relevant to the subject, click on the appropriate country flag to get more details of the book or to buy it from them.

cover Introduction to 3D Game Programming with DirectX 9.0 - This is quite a small book but it has good concise information with subjects like, maths introduction and picking.

cover If you are interested in 3D games, this looks like a good book to have on the shelf. If, like me, you want to have know the theory and how it is derived then there is a lot for you here. Including - Graphics pipeline, scenegraph, picking, collision detection, bezier curves, surfaces, key frame animation, level of detail, terrain, quadtrees & octtrees, special effects, numerical methods. Includes CDROM with code.

This book contains more mathematically rigorous methods for picking than described above.

Other Math Books

Terminology and Notation

Specific to this page here:

 

This site may have errors. Don't use for critical systems.

Copyright (c) 1998-2023 Martin John Baker - All rights reserved - privacy policy.