This page covers static forces, if the objects start moving then we need to use differential equations.
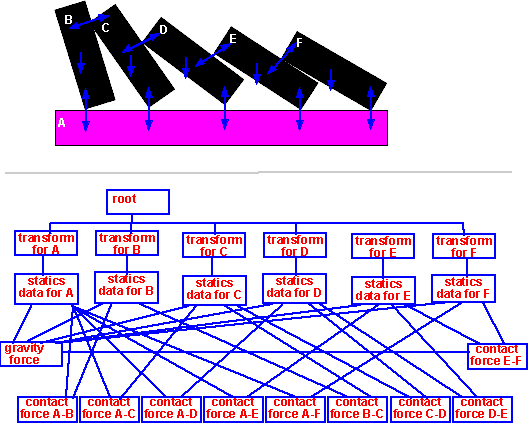
In most 3d modeling programs, shapes can be moved around and will be able to pass through each other. However in a physics modeling program we need a way to prevent solid objects from occupying the same space. We also need to know whether objects are in equilibrium, or whether they are going to start accelerating in some direction. To do this, we need to model forces. Is there any way that this can be done by the program itself from its database of the properties of objects in its world, without being explicitly told about where the forces are acting?
This seems like a difficult problem and this page tries to work out some of the general rules. If this approach is not possible then it may be simpler to model the system by explicitly defining a framework of solid objects and joints as on the next page.
Forces
Forces acting on the 'centre of mass' c-of-m can be added using vector addition. Torque's (Force times distance) tending to cause rotation can also be added.
Gravity
This acts on the c-of-m in the -y direction. If an object is resting on the earth (for this purpose assume the earth is an object with infinite mass) and its c-of-m is above its base, then there is not much point in working out the forces (unless there is enough sideways force to overcome friction or knock it over) and the object can be marked as 'at rest'.
This also applies to objects on top of objects on the ground.

When a sideways force is applied to an object on the ground, then it may slide depending on the friction coefficients, if not the force may be strong enough to tip it up. When the c-of-m is outside the base then it will start to fall.

Rotational Forces
The mathematics of rotations is explained on this page. This physics of rotations is discussed on this page.
The following terms are associated with rotational forces:
Torque
When two, or more, forces are acting on a solid body and the forces are not acting in line then there may be an overall turning effect. Where a force tries to move an object in a linear way a torque tries to turn the object. The torque is measured about a particular point on a solid object. The magnitude of the torque, about this given point, depends both on the magnitude and direction of the forces and there distance from the point.
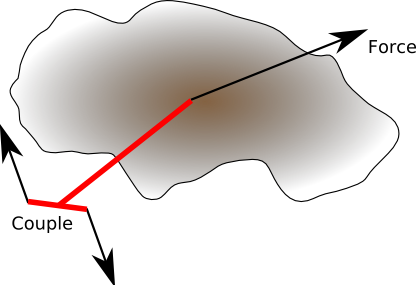
Couple or Moment
This is a system of forces that tries to produce a rotation only. That is the forces are balanced so that there is no overall linear force.
A system of forces, acting on a solid object, can be resolved into a couple and a linear force. If the resultant of all forces and couples is not zero the object will move.
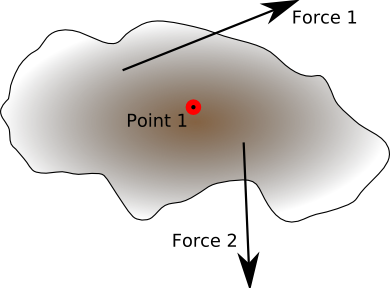
We can resolve an arbitrary system of forces into a single couple and single force.
- To find the resultant force we take the vector sum of the forces without taking account the points at which the force acts.
- To find the resultant couple, about some convenient point (point 1) such as the centre of mass, we take the vector sum of the cross product of the force with its distance from the point (F x r).
If the system of forces are in balance, then the point that we choose to measure the couple around is just a matter of choosing the most convenient point for the calculations. This is because, if it is in balance around one point, it is in balance around all points. However, if the forces are not in balance, it is important and we will want to find the axis where the couple can be consided to act.
Parallel Axis Theorm
We can convert one system of forces into an equivalent system of forces.
Screws
A system of forces can be represented by Screw Theory. This allows us to apply transforms to the combination of linear and rotational quantities is a simpler way.
| Combined Linear and Rotational Quantity | Represents | Requires |
|---|---|---|
| wrenches | force and torque | two vectors |
| twists | velocity | four line coordinates |
Other Forces
Other forces may be modeled, such as springs, electromagnetic, etc. These are covered in further sections.