3D Physics - Machines

In this case a 'machine' is any device where you can apply a force to move some object.

Law of the Machine

For an ideal machine

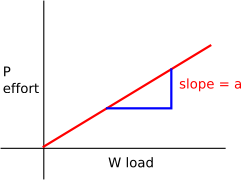
P=a W

where:		other definitions
symbol	description	type	units
P	effort	vector	N=newton=kg*m/s2
W	load	vector	N=newton=kg*m/s2
a	slope	scalar	none

For a machine with friction

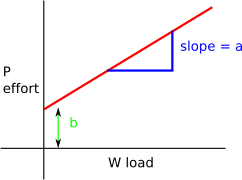
P=a W + b

where:		other definitions
symbol	description	type	units
P	effort	vector	N=newton=kg*m/s2
W	load	vector	N=newton=kg*m/s2
a	slope	scalar	none
b	static friction	vector	N=newton=kg*m/s2

Limiting Mechanical Advantage and Efficiency

M.A. = W/P

but P=a W + b so,

M.A. = W/(a W + b)

M.A. = 1/(a + b/W)

As W is increased b/W becomes smaller. At high values of W, b/W becomes practically zero. The M.A. is said to reach a limiting value when W is infinitely large.

Limiting M.A. = 1/a

Limiting efficency = Limiting M.A./VR = 1/(a * VR)

This is the limiting efficiency which can be attained by a machine

Example

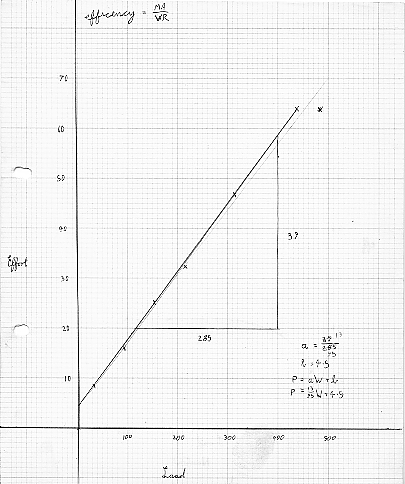
A simple lifting machine gave the following results on test:

Load Raised (N)	30.2	93.4	155.8	218	311.8	438
Effort Applied (N)	8.45	16	25.1	32.2	46.7	63.7

Plot these values and find the law of the machine.

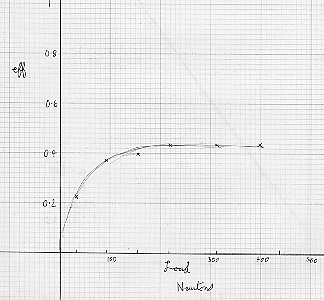
Draw the efficiency on a load base. What is the limiting efficiency? VR = 15.75

1. efficiency = 30.2/(8.45*15.75) = 0.246 at 30.2N (load)
2. efficiency = 93.4/(16*15.75) = 0.37 at 93.4N (load)
3. efficiency = 155.8/(25.1*15.75) = 0.393 at 155.8N (load)
4. efficiency = 218/(32.2*15.75) = 0.431 at 218N (load)
5. efficiency = 311.8/(46.7*15.75) = 0.424 at 311.8N (load)
6. efficiency = 438/(63.7*15.75) = 0.437 at 438N (load)

 

EuclideanSpace

home

Standards