Physics - Dynamics Rotation - Inertia Tensor

Conservation of Angular Momentum

For any closed system this total angular momentum is constant.

At first this seems counter intuitive, it is easy to think of a mechanism that converts rotation in one dimension to rotation in another dimension, or converts between linear and rotational motion:

gears

However, angular momentum is still conserved in every dimension for a closed system.

Inertia Tensor

We have already seen that that linear momentum is conserved for a closed system but momentum can be exchanged between objects within the closed system by means of equal and opposite forces. In the same way angular momentum can be exchanged between object within a closed system by means of equal and opposite torques.

The relationship between torque and the acceleration can be expressed in the following tensor equation:

torque = T = [I]α

where:
symbol
description
type
units
T torque vector Nm = Kg m²s-2
[I] inertia tensor tensor Kg m²
α angular acceleration vector s-2

This can be expressed in terms of the exchange of angular momentum as follows (by integrating both sides of the torque equation over time):

angular momentum = L = [I]ω

where:
symbol
description
type
units
L angular momentum vector Nm = Kg m²s-1
[I] inertia tensor tensor Kg m²
ω angular velocity vector s-1

So the inertia tensor plays a similar role in angular equations as mass does in linear equations. However the inertia tensor is a lot more complicated.

Inertia Tensor in 2D

We can't have rotations in one dimension so two is the lowest number of dimensions to which we can apply this. In two dimensions the inertia tensor is a scalar quantity known as the second moment of mass.

I = ∫(r²)dm

In other words, we don't just sum the mass, but mass further from the rotation axis has more effect. Each element of mass is multiplied by the square of its distance from the centre of rotation.

Inertia Tensor in 3D

In 3 dimensions the inertia tensor is grade 2, which is a matrix. This makes things a bit more complicated as it means that a torque, say around the 'x' axis, can cause acceleration around the other axes.

[I] =
∫(rz²+ry²)dm -∫rx*rydm -∫rx*rzdm
-∫ry*rxdm ∫(rz²+rx²)dm -∫ry*rzdm
-∫rz*rxdm -∫rz*rydm ∫(rx²+ry²)dm

The inertia tensor is derived on this page.

This matrix is symmetrical around the leading diagonal and it has the property that it can be factored into rotational and diagonal parts as follows:

[I] = [R][D][Rt]

where:

Factoring matrices in this way is discussed on this page. What this means, in practical terms, is that we can always rotate the local coordinates of the solid object in such a way that [I] becomes a diagonal matrix. Which means that, in this axis, the acceleration will be around the same axis as the torque.

Another way of explaining this is that, there are certain symmetries of any solid object around which it will rotate without wobbling into a different axis. These symmetrical axes are the eigenvectors of [I].

Rotating Coordinate Bases

Above we saw above the inertia tensor varies as we rotate the basis vectors according to the formula: [I] = [R][D][Rt]

So how can we derive this result? One approach is to note that the inertia tensor has a quadratic form (for more about quadratic form see this page or box on right). Since it has a quadratic form we can split out the basis vectors as row and column vectors like this:

x y z
ixx ixy ixz
iyx iyy iyz
izx izy izz
x
y
z

So lets check what happens when we rotate these coordinate vectors. We can easily rotate the column vector by multiplying by a rotation matrix:

r r r
r r r
r r r
x
y
z

So how do we rotate the row vector? We can use the rule for matrix multiplication:

[M1 * M2]t = [M2]t * [M1]t

where the t superscript means transpose. In other words, to multiply the transpose of two matrices we reverse the order and get the transpose of the whole thing:

x y z
r r r
r r r
r r r
t

So making these two substitutions for the rotation vectors we have:

x y z
r r r
r r r
r r r
t
ixx ixy ixz
iyx iyy iyz
izx izy izz
r r r
r r r
r r r
x
y
z

So the inertia tensor part of the equation becomes:

r r r
r r r
r r r
t
ixx ixy ixz
iyx iyy iyz
izx izy izz
r r r
r r r
r r r

Note the leading rotation matrix is transposed unlike the equation above. This is because here we are rotating the coordinate bases and keeping the object stationary, whereas above we are rotating the object in a fixed coordinate system, so the the rotations are reversed.

Inertia Tensor in n dimensions

I don't know what form the inertia tensor would take in higher dimensions?

Inertia Tensor using Quaternions

Is it possible to use quaternions (spinors) to represent the 3D inertia tensor? I guess there may be some way to do it but for it to be useful it would be best if it were done using the sandwich product.

T = q*α*conj(q)

As we have seen the inertia tensor can be factored into rotational and diagonal parts as follows:

[I] = [R][D][Rt]

We already know that we can represent the rotational parts [R] and [Rt] by using a quaternion so the question is: can we represent a diagonal matrix [D] using a quaternion 'q' ? By using the matrix representation of the sandwich product:

Pout.w
Pout.x
Pout.y
Pout.z
=
q.w²+q.x²+q.y²+q.z² 0 0 0
0 q.w²+q.x²-q.y²-q.z² 2*q.x*q.y - 2*q.w*q.z 2*q.x*q.z + 2*q.w*q.y
0 2*q.x*q.y + 2*q.w*q.z q.w²-q.x² + q.y²-q.z² 2*q.x*q.z - 2*q.w*q.x
0 2*q.x*q.z - 2*q.w*q.y 2*q.y*q.z + 2*q.w*q.x q.w²-q.x²-q.y²+q.z²
Pin.w
Pin.x
Pin.y
Pin.z

For this to be diagonal, then the non-diagonal terms must be zero:

q.x*q.y - q.w*q.z = 0
q.x*q.y + q.w*q.z = 0
q.x*q.z + q.w*q.y = 0
q.x*q.z - q.w*q.y = 0
q.x*q.z - q.w*q.x = 0
q.y*q.z + q.w*q.x = 0

rearranging gives:

q.w*q.z = - q.w*q.z
q.w*q.y = - q.w*q.y
q.w*q.x = - q.w*q.x

There is a solution where q.x = q.y = q.z = 0 but that is not very useful as it just gives a scaling matrix. I can't see any other solutions so I conclude that we cant use quaternions to represent inertia tensors. I don't know if the more general multivectors can be used to represent inertia tensors? I have seen it said that the inertia tensor is not orthogonal and therefore cant be replaced by a spinor - is this correct?

Steady State Motion

When a solid object is moving in empty space with no external forces acting on it, then we can consider its linear velocity and its angular velocity independently:

So here is a difference between linear and angular motion, with linear motion (provided there is no air resistance) it can move in all directions equally, regardless of the shape of the object. With rotation the direction of spin may be dependent on the orientation of the object (and visa versa).

There are other differences between linear motion and rotation, for instance, Newtonian laws can be applied in local coordinates when the local frame of reference has linear motion. However Newtonian laws don't work on a rotating frame of reference.

When we are dealing with rotation, some of these laws are not immediately initiative, there is no reason to give gyroscopes, for example, mystical significance, they are obeying simple laws (even if I don't claim to fully understand them yet!). However we can be fooled by our intuition into misunderstanding these rules. I am therefore collecting some simple examples here, table top physics, to help us get an initiative understanding. For example, too think about how an object rotates about its principle moment of inertia, see the egg example.

Non-Steady state conditions

What happens if a force, torque or impulse is applied to the steady state case above?

So in these cases we can still deal with the linear and angular quantities independently, but what about:

In these cases both the linear and angular qualities will be affected, however in both cases, we could find an equivalent force/torque combination applied to the centre of mass. In other words, a linear force applied to some point on the object other than the centre of mass will be equivalent to some force on the centre-of-mass plus some torque about the centre of mass. However these equivalents may vary with time, for example a linear force on the outside of a rotating wheel may produce a sinusoidally varying torque.

Another possibility is that a torque is applied to a nonsymmetrical object, in a direction not along a principle moment of inertia. This will cause the object to accelerate in the direction of the torque. However any angular velocity, not along the principle moment of inertia will generate another torque, at a different angle to the first, this will tend to rotate the object to make its principle axis of inertia line up with the applied torque.

To try to get an initiative understanding of this, see the egg and pencil-at-45degrees examples. This is also the principle of procession (gyroscopes).

Can anyone help me derive a generalised set of mathematical equations for this?

No External Torque

What are the equations for the movement of a rigid object with no external forces or torques acting on it?

This is the simplest case that I can imagine for a simulation which includes rotation, so I would like to make sure that I fully understand it and can represent it programmatically before going on to more complex situations like collisions and jointed structures.

For a rigid object rotating in free space, by Newtons first law (and Euler for rotation):

So the linear position of the centre of mass is given by:

[p] = [p0] + [v]t

where:
symbol
description
type
units
[p] position vector in x,y and z dimensions vector m
[p0] position vector at t=0 vector m
[v] velocity vector vector m/s
t t = time () scalar s

For the rotation component the situation is more complex:

[angle] may not equal [angle0] + [w] t

This is because vector algebra on angles does not represent the way that angles are combined in the 3D world (see here for details).

However infinitesimal rotations, and hence angular velocities, can be combined using vector algebra, so if the transform matrix is given by:

[R] =
c θ *c φ -c θ *s φ s θ
cψ*sφ + s ψ* s θ*c φ cψ*cφ -s ψ*s θ*s φ -s ψ*c θ
sψ*sφ - c ψ* s θ*c φ sψ*cφ + c ψ*s θ*s φ c ψ*c θ

Then the angles can be replaced by the following functions of time:

These components of angular velocity in the x,y and z dimensions can be considered independent and be combined as required.

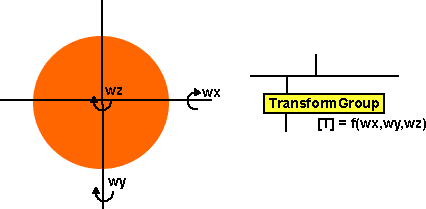
So the three components can be added to give a rotation about any axis.

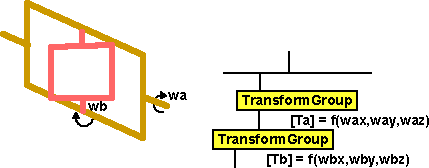
Another way to combine rotations is where one rotation rotates the frame-of-reference of a second object which is rotating relative to the frame-of-reference.

This is putting the transform group of one object under a second transform group. A combined transform group can be calculated by multiplying the two transform matrices.

This can lead to some complex term in the resultant matrix. This is due to the complex motion generated, examples are the motion of the moon around the earth around the sun, or the gimbals holding a gyroscope.

The conservation of momentum laws may not apply relative to the rotating frame-of-reference.

 

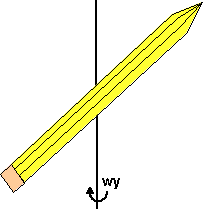
Can a free floating object spin in any direction?

A spherical object can rotate in any dimension, but what about an asymmetric object?

To illustrate this, think of a pen or pencil inclined at 45 degrees to the y-axis. If we apply an external torque we can get it to rotate about the y-axis (i.e. at 45 degrees to its long axis). But if we remove the external torque, will it continue to rotate in this way?

In the interests of science, I have been experimenting an throwing pens in the air. I cant get it to rotate in this way, as soon as it leaves my hand it just wants to rotate about its short axis (i.e. with the pointed end and the eraser on the outside of the spin).

I can get the pen to spin about its short axis or its long axis, but not in-between.

I think I can get it to spin about both these axis at the same time (its difficult to be sure as my eyes aren't fast enough). but what appears to be happening is that it is rotating pointed end over eraser, and then it is spinning about its long axis which is rotating itself. So it appears to be making a complex rotation, as described above, of a rotation within a rotation.

So what are the allowed modes of

Some answers from Yaakov Eisenberg, thank you for this - Martin :

> What if it were being forced to rotate in this direction and then the external
> forces were suddenly switched off, would it, at that instant suddenly start
> spinning only about its various axis?)

Yes, it would instantly start to rotate about a different axis, but the change is not as discontinuous (therefore, unrealistic) as it might seem. The velocities of the masses change continuously; only their accelerations change discontinuously, due to the discontinuous change in the force.

> So given a generalised inertia matrix, what are the conditions for an object
> to be able to rotate about any given axis?

When rotating about the axis, the object's angular momentum vector must be parallel to the axis (i.e., parallel to the object's angular velocity vector). If this is the case, the axis of rotation will remain constant in time. Otherwise, it won't.

For any object, there are at least three axes for which this is true. They are called the object's principal axes, and the inertia matrix is diagonal in the coordinate system defined by them. If the object is sufficiently symmetric, there will be more than three.

> Is it that single rigid object
> without external forces can never have centrifugal forces (because of
> Newtons-Eulers first law)?

I think this is also a correct way of stating it.

rotation for any object?

Gyroscopes, Precession and Nutation

I don't think these effects are applicable here, as gyroscope affects only apply if there is an external torque. However if there are small external torques from say, wind effects, then we would need to take these effects into account.

Polhodes

KErot = (1/2) {w}T [Ig] {w}

{Tg} = [Ig] {w}

where:
symbol
description
type
units
KErot rotational kinetic energy scalar  
w angular velocity bivector  
[Ig] Inertia matrix 3x3 matrix  
TG torque about centre of gravity bivector  
{} vector in x,y and z dimensions    
{}T transpose of vector in x,y and z dimensions    

This gives:

KErot = (1/2) I* w^2

where:

note I* is not constant, its value changes as the angular velocity changes

Principal Moments of Inertia

To find the principle moments of inertia we need to find the eigenvalues of the inertia matrix.

From this:

(m11- λ) (m22- λ) (m33- λ) + m12 m23 m31 + m13 m21 m32 - (m11- λ) m23 m32 - m12 m 21 (m33- λ) - m13 (m22- λ) m31 = 0

 

substituting the inertia values into this gives:

 

(Ixx- λ) (Iyy- λ) (Izz- λ) - 2 Ixz Ixy Iyz - (Ixx- λ) Iyz^2 - (Izz- λ)Ixy^2 - (Iyy- λ) Ixz^2 = 0

This is a third order equation in L, which may give 3 values for λ.

The values of λ are the eigenvalues, which are the principle moments of inertia.

Examples:

In order to simplify the maths, I will try a few examples using 2D matrices, we are still considering 3D rotations but all the masses are in the z=0 plane.

Example 1

First consider a rigid body with most of its mass at +1 and -1 on the y plane.

Ixx = sum (y^2)dm = 1+1=2

Iyy = sum(x^2) dm = 0

Ixy = sum(x*y)dm =0

det[M] = Ixx Iyy - Ixy Ixy = 0-0 =0

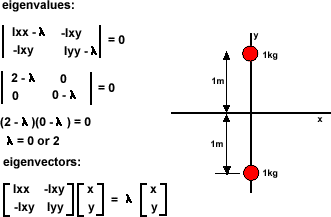
(Ixx - λ)*x = Ixy * y

x/y = Ixy /(Ixx - λ)

for λ=0

x/y = 0/2=0

normalising gives a unit vector in the x direction {1,0}T

for λ=2

x/y = 0/0=?

using the bottom equation

(Iyy - λ)*y = Ixy * x

y/x = Ixy/(Iyy - λ)

for λ=0

y/x = 0/0 = 0

for λ=2

y/x = 0/(0-2)=-0.5

normalising gives a unit vector in the y direction {0,1}T

Example 2

Next consider a rigid body with most of its mass at 45 degrees to the y plane.

Ixx = sum (y^2)dm = 0.5+0.5 = 1

Iyy = sum(x^2) dm = 0.5+0.5 = 1

Ixy = sum(x*y)dm =0.5+0.5 = 1

det[M] = Ixx Iyy - Ixy Ixy = 0.25-0.25 =0

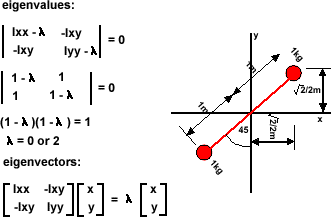
x/y = Ixy /(Ixx - λ)

for λ=0

x/y = 1/(1-0) = 1

normalising gives a unit vector at 45 degrees (along the line joining the masses).

for λ=2

x/y = 1/(1-2) = -1

normalising gives a unit vector at -45 degrees (at 90 degrees to the line joining the masses)

Example 3

Next consider a rigid body with 3 equally spaced masses:

Ixx = sum (y^2)dm = 1+sin(30)^2+sin(30)^2 = 1.5

Iyy = sum(x^2) dm = cos(30)^2 + cos(30)^2 = 0.75 + 0.75 = 1.5

Ixy = sum(x*y)dm = sin(30) * cos (30) - sin(30) * cos (30) = 0

det[M] = Ixx Iyy - Ixy Ixy = 1.5*1.5 = 2.25

 

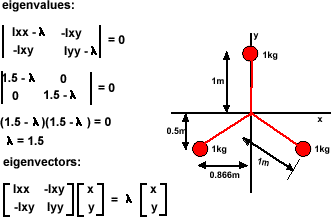
for λ=1.5

x/y = 0/(1.5-1.5) = 0/0 = undefined.

Inertia Ellipsoid

So the above examples show that the inertia matrix defines how an object can spin if there is no external torque.

If the terms of the leading diagonal are all equal and all other terms are zero then, the object can spin in any direction and all directions of spin will have the same inertia. In this case the eigenvalues will all be equal to each other and to the inertia. The eigenvectors will be undefined.

 

If the terms of the leading diagonal are not equal and all other terms are zero then, the objects inertial coordinates are aligned with its axis of rotation. It may spin about the x,y or z axis but it will prefer to spin about the axis with the highest inertia. In this case the eigenvalues will have different values which will be the values of the inertia terms in the leading values. The eigenvectors will be in the direction of the x,y and z axis.

If the non leading diagonal terms are zero then, the objects inertial coordinates are not aligned with its axis of rotation. In this case the eigenvalues will have the values that the leading diagonal would have if the inertial coordinate frame were rotated to align with the rotation axis. The eigenvectors will be in the direction of rotation axis.

Applications

We try to use this to simulate the physical world on this page.

metadata block
see also:

 

Correspondence about this page

Book Shop - Further reading.

Where I can, I have put links to Amazon for books that are relevant to the subject, click on the appropriate country flag to get more details of the book or to buy it from them.

 

cover Game Physics - This book has some useful stuff, its more of a textbook, not a step by step guide (although it does have a disc with a lot of C++ code). About the first third of the book is a physics textbook with theoretical exercises, the middle bit covers physics engine topics, and the last third of the book covers mathematical topics. I think I would use this book as a reference book to lookup the theory behind something I might be working on rather than a book to work through in order.

Commercial Software Shop

Where I can, I have put links to Amazon for commercial software, not directly related to the software project, but related to the subject being discussed, click on the appropriate country flag to get more details of the software or to buy it from them.

 

This site may have errors. Don't use for critical systems.

Copyright (c) 1998-2023 Martin John Baker - All rights reserved - privacy policy.