Physics - Dynamics - Combined Linear and Rotational quantities

In the linear only case:

J = Vcm * m

where:

so the velocity change is J/m in the same direction as the impulse.

In the rotational case we can take the impulse equivalent of torque

2D case (using x and y components) 3D case (using vector equations)
'impulse torque' = Jx * ry - Jy * rx = I * w 'impulse torque' = r × J= [I]w

Combined Linear and Rotational

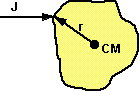
If the impulse is not in line with the centre of mass then there will be a change to both the linear and rotational velocity of the object. The aim is to derive an equation for the total change in velocity of a particle on a solid body due to an impulse on that point.

As described in the kinematics section the velocity of a point on a solid body is given by:

2D case (using x and y components) 3D case (using vector equations)
Vpx = Vcmx - ry w
Vpy = Vcmy + rx w 		Vp = Vcm + w × r

where:

We can write this equation in terms of changes to velocities:

2D case (using x and y components) 3D case (using vector equations)
Vpx = Vcmx - ry w
Vpy = Vcmy + rx w

The component of linear velocity due to rotation is: v vector = w vector x r vector as derived here. so the change in linear velocity will be:

Vp = Vcm + w x r

Where:

This consists of a linear component and a rotational component.

For the linear component, as explained above,

linear impulse = J = Vcm * M

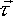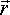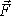For the rotational component, since torque vector= r vector x force vector as defined here, then integrating both sides over the time of collision gives:

'impulse torque' = r × J= [I]w

where:

[I] = inertia tensor

This inertia tensor is a 3x3 matrix and since the other terms in this equation are defined in absolute coordinates the inertia tensor is defined in absolute coordinates, this means that the elements of the inertia tensor may be time dependant.

This makes the equations very complicated, so to simplify things we will start by using a single scalar value for I, this will only be valid for symmetrical objects but we can use this simple case for now, this gives:

w = (r x J)/I

where:

I = inertia scalar such that torque = I * alpha (only true when object is symmetrical)

Substituting these impulse expressions into the expression for the particle velocity gives:

2D case (using x and y components) 3D case (using vector equations)
Vpx = Jx/m - ry (Jx ry - Jy rx) /I
Vpy = Jy/m + rx (Jx ry - Jy rx) /I		 Vp = J/M + ((r × J) × r)/I

For the 2D case

We want to get an expression for J so we can start by grouping together the Jx and the Jy terms:

Vpx = Jx ( 1/m - ry2/I) + Jy rx ry / I
Vpy = Jx rx ry / I + Jy ( 1/m - rx2/I)

Solving this for J gives:

Jx = (m/(1/m - rx2/I - ry2/I))*(Vpx ( 1/m - rx2/I) -Vpy rx ry / I )
Jy = (m/(1/m - rx2/I - ry2/I))*(-Vpx rx ry / I + Vpy ( 1/m - ry2/I))

For the 3D case

Again we want to solve for J, One option is to use the triple product identity which gives:

Vp = J/M + (-r(J•r) + J(r•r))/I

Collecting the terms, this gives one part in the direction of impulse (J) vector and another part in the direction of vector r:

Vp = J( 1/M +(r•r)/I) - r(J•r)/I

As required J produces a greater velocity change if there is both linear and rotational motion. (thanks to databeaver for helping me out here)

Special cases

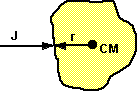If J and r are parallel then the J(r•r)/I and r(J•r)/I terms cancel out and we get the one dimensional case as expected:

Vp = J/M

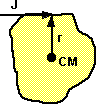If J and r are at 90 degrees then J•r is zero and the equation becomes:

Vp = J( 1/M +(r•r)/I)

Again the change in velocity is in the direction of the impulse.

In both the above special cases Vp will be in line with the impulse J, but for cases in-between there will be a component in the direction of r, this means that an impulse in one direction can cause a change in velocity in a different direction (even when the object is symmetrical).

 

I would still like to get a more general solution for 3x3 inertia tensor,

Vp = J/M + ([I]-1(J × r)) × r

where:

[I]-1 = Inverse of inertia tensor (3x3 matrix)

Alternative method using matrices

It seems like a good idea to express all terms using the same type of algebra, it is not possible to express inertia tensor purely in terms of vectors or quaternions so can we calculate purely in terms of matrices?

We can convert the vector cross product to a skew matrix as shown here.

vector equation matrix equation  
J × r
0 rz -ry
-rz 0 rx
ry -rx 0
Jx
Jy
Jz
[I]-1(J × r)
ixx ixy ixz
iyx iyy iyz
izx izy izz
0 rz -ry
-rz 0 rx
ry -rx 0

multiplying out the terms gives:

-ixy*rz + ixz*ry ixx*rz - ixz*rx -ixx*ry + ixy*rx
-iyy*rz + iyz*ry iyx*rz - iyz*rx -iyx*ry + iyy*rx
-izy*rz + izz*ry izx*rz - izz*rx -izx*ry + izy*rx
Jx
Jy
Jz
([I]-1(J × r)) × r
-ixy*rz + ixz*ry ixx*rz - ixz*rx -ixx*ry + ixy*rx
-iyy*rz + iyz*ry iyx*rz - iyz*rx -iyx*ry + iyy*rx
-izy*rz + izz*ry izx*rz - izz*rx -izx*ry + izy*rx
0 rz -ry
-rz 0 rx
ry -rx 0

multiplying out the terms gives:

-(ixx*rz - ixz*rx)*rz + (-ixx*ry + ixy*rx)*ry (-ixy*rz + ixz*ry)*rz - (-ixx*ry + ixy*rx)*rx -(-ixy*rz + ixz*ry)*ry + (ixx*rz - ixz*rx)*rx
-(iyx*rz - iyz*rx)*rz + (-iyx*ry + iyy*rx)*ry (-iyy*rz + iyz*ry)*rz - (-iyx*ry + iyy*rx)*rx -(-iyy*rz + iyz*ry)*ry + (iyx*rz - iyz*rx)*rx
-(izx*rz - izz*rx)*rz + (-izx*ry + izy*rx)*ry (-izy*rz + izz*ry)*rz - (-izx*ry + izy*rx)*rx -(-izy*rz + izz*ry)*ry + (izx*rz - izz*rx)*rx

combining the terms gives:

-ixx*rz*rz + ixz*rx*rz -ixx*ry*ry + ixy*rx*ry -ixy*rz*rz + ixz*ry*rz +ixx*ry*rx - ixy*rx*rx ixy*rz*ry - ixz*ry*ry + ixx*rz*rx - ixz*rx*rx
-iyx*rz*rz + iyz*rx*rz -iyx*ry*ry - iyy*rx*ry -iyy*rz*rz + iyz*ry*rz + iyx*ry*rx - iyy*rx*rx iyy*rz*ry - iyz*ry*ry + iyx*rz*rx - iyz*rx*rx
-izx*rz*rz + izz*rx*rz -izx*ry*ry + izy*rx*ry -izy*rz*rz + izz*ry*rz + izx*ry*rx + izy*rx*rx izy*rz*ry - izz*ry*ry + izx*rz*rx - izz*rx*rx
Jx
Jy
Jz

Change in linear velocity of a point on a solid body due to J=

J/M + ([I]-1(J × r)) × r
-ixx*rz*rz + ixz*rx*rz -ixx*ry*ry + ixy*rx*ry + 1/M -ixy*rz*rz + ixz*ry*rz +ixx*ry*rx - ixy*rx*rx ixy*rz*ry - ixz*ry*ry + ixx*rz*rx - ixz*rx*rx
-iyx*rz*rz + iyz*rx*rz -iyx*ry*ry - iyy*rx*ry -iyy*rz*rz + iyz*ry*rz + iyx*ry*rx - iyy*rx*rx + 1/M iyy*rz*ry - iyz*ry*ry + iyx*rz*rx - iyz*rx*rx
-izx*rz*rz + izz*rx*rz -izx*ry*ry + izy*rx*ry -izy*rz*rz + izz*ry*rz + izx*ry*rx + izy*rx*rx izy*rz*ry - izz*ry*ry + izx*rz*rx - izz*rx*rx + 1/M
Jx
Jy
Jz

Where;

Kinetic Energy of Solid Body

Kinetic Energy is a scalar quantity for any system (as described here).

For purely linear motion the kinetic energy of a solid body is:

T = 0.5 m v2

For purely rotational motion the kinetic energy, about its centre of mass, of a solid body is:

T = 0.5 wt [I] w

So if we have combined linear and rotational motion can we just add the kinetic energy due to these parts separately? I think the answer is no because the energy of a particle is proportional to the square of its velocity. We need to add on another factor:

T = 0.5 m v2 + 0.5 wt [I] w + m(v•(w x r))

This can be derived as follows:

T for particle on solid body = 0.5 sum(mi vi2 )

but the velocty of a particle on a solid body is (v + w x r) so the kinetic energy is:

T = 0.5 sum(mi (v + w x r)•(v + w x r))

this can be expanded out to give:

T = 0.5 sum(mi (v2 + (w x r)•(w x r) +2v•(w x r))

So, there is a part that is due purely to linear motion, a part that is due purely to rotational motion, and a part that is due to the product of linear motion and rotational motion.

 

 

 

Example

Imagine a theoretical solid object made up of two masses as follows:

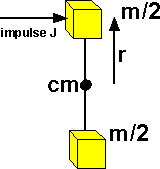
Immediately after the collision the change in linear velocity of the top object will be:

vf - vi = 2*J/m

and the bottom object will be 0.

So the linear velocity of the centre of mass (cm) will be:

vf - vi = J/m

The angular velocity in radians can be calculated from this by using v = w × r , so w will be: (linear velocity of cm) / r

angular velocity change = w = J/(m*r)

where:

Strictly we cant divide by a vector so we should really write this as:

angular velocity change = wc = J × r-1 /m

It may seem strange that if the impulse is applied at the top then it will produce the same linear velocity as when applied at the centre but with additional rotational velocity. At first thought this may seem to contradict the conservation of energy, but conservation of energy is a completely different issue, for instance if the collision occurs at the outside of the object, there will be less to push against, so the impulse will be less.

So far this is a special case which is made up of two masses, in order to make this more general we want to work in terms of the moment of inertia (or if we are working in 3D the inertia tensor), this is:

inertia = I = sum(r2 m)

angular momentum = L = Iw

so,

angular momentum change = Lc = Iwc

Lc = Iwc = r × J

so,

wc = I-1(r × J)

where:

I-1= inverse moment of inertia function

metadata block
see also:

 
Correspondence about this page

Book Shop - Further reading.

Where I can, I have put links to Amazon for books that are relevant to the subject, click on the appropriate country flag to get more details of the book or to buy it from them.

 

cover Game Physics - This book has some useful stuff, its more of a textbook, not a step by step guide (although it does have a disc with a lot of C++ code). About the first third of the book is a physics textbook with theoretical exercises, the middle bit covers physics engine topics, and the last third of the book covers mathematical topics. I think I would use this book as a reference book to lookup the theory behind something I might be working on rather than a book to work through in order.

Commercial Software Shop

Where I can, I have put links to Amazon for commercial software, not directly related to the software project, but related to the subject being discussed, click on the appropriate country flag to get more details of the software or to buy it from them.

 

cover Dark Basic Professional Edition - It is better to get this professional edition

cover This is a version of basic designed for building games, for example to rotate a cube you might do the following:
make object cube 1,100
for x=1 to 360
rotate object 1,x,x,0
next x

cover Game Programming with Darkbasic - book for above software

This site may have errors. Don't use for critical systems.

Copyright (c) 1998-2023 Martin John Baker - All rights reserved - privacy policy.