Here we are looking at the collision of rigid objects and how to calculate the response. There are a number of theoretical and practical issues that we need to consider, on this page we will start looking at the equations we get in collisions with combined rotation and linear motion, subpages look at the two and three dimensional cases in more detail. The way that momentum is transferred by an impulse is discussed on this page.
On this page we discuss more about the practical factors such as:
- Whether we model the deformation of the objects or whether we assume solid body collisions.
- What assumptions we make about elasticity coefficient and energy converted to heat.
- What assumptions we make about friction and how objects slide.
- How we handle multiple points of contact and simultaneous collisions.
There is no right answer to these questions, it depends on factors like: what we want to do, what accuracy do we need, how much computer power do we have, how stable must the simulation be and what type of materials are we dealing with.
Combined Rotation and Movement with a Linear Motion
It is difficult to analyse the situation when the colliding objects are free to both rotate and move with a linear motion. The main method we will use to do this involves the following stages.
- Determine the collision point and the normal direction at this point.
- Calculate the minimum impulse to prevent the objects intersecting, or to
reverse the approach velocity, depending on the coefficient of friction. - Calculate the effect of this impulse on the rotation and linear motion
separately.
This involves a lot of assumptions and approximations that may not always be valid, we need to understand what is going on to be sure that our simulations or programs are making the correct assumptions and that the results will be stable and accurate enough.
This method is based on the concept of an 'impulse' which is an instantaneous transfer of momentum between the objects. This is not intuitively obvious and I think its worth taking some time to rid ourselves of our natural misconceptions. The collision may involve an exchange of energy between the objects but the impulse is about momentum not energy, this distinction means:
- Momentum is a vector quantity in which all the dimensions are independent and the linear dimensions are independent of the rotational dimensions.
- Linear momentum and rotational momentum for a closed system are conserved independently, that is, linear momentum cannot be converted to rotational momentum and visa versa. Energy can be converted into other forms.
- The component of momentum in each dimension for a closed system is conserved independently, that is, the x component of momentum cannot be converted to, or from, the y component of momentum. Again energy can be converted into other forms.
- The whole of the impulse causes changes the linear momentum and rotational momentum, it is not that part of the impulse applies to linear momentum and the rest applies to rotational, all the impulse applies to both. In the case of energy we can ascribe part of the energy to the linear motion and another part to the rotational motion and energy can be transferred between them.
This last point is difficult for people to understand, it took me a long time for me to realise this and I have found that many other people have problems with it. This seems like something for nothing, the same impulse doing two jobs, but its not. The impulse just exchanges momentum between two objects and the same impulse can transfer the two types of momentum. Its not the same as energy and it works completely differently.
If you would like to see a practical example of this see this page (sent to me by Kevin Pegrume) which demonstrates this and highlights some of the counter intuitive issues.
Results
Here are equations for calculating the components of impulse (J) then the equations to use this to calculate the new velocities. This is just an overview, the definitions and derivations are given on the individual pages for the one, two and three cases:
The results for the one dimensional case (no rotation) are as follows: (see this page for code and derivation)
|
General Case (between Perfectly elastic and Perfectly inelastic) |
|
| coefficient of restitution | e = ( |
| impulse = | (e+1)*( |
| Final velocity of object a= |
|
| Final velocity of object b= |
The results for the two dimensional case are as follows: (see this page for code and derivation)
| General Case (between Perfectly elastic and Perfectly inelastic) | |
| impulse = |
Jx = (e+1)/k * (Vaix - Vbix)( 1/ma - rax2/Ia + 1/mb - rbx2/Ib)
- (e+1)/k * (Vaiy - Vbiy) (rax ray / Ia + rbx rby / Ib) where: k=1/ma2+ 2/ma mb +1/mb2 - rax2/maIa - rbx2/maIb - ray2/maIa - ray2/mbIa - rax2/mbIa - rbx2/mbIb - rby2/maIb - rby2/mbIb + ray2 rbx2/IaIb + rax2 rby2/IaIb - 2 rax ray rbx rby/IaIb |
| Final velocity of object a= |
Vaix - Jx/Ma Vaiy - Jy/Ma |
| Final velocity of object b= |
Vbix - Jx/Mb Vbiy - Jy/Mb |
| Final angular velocity of object a=waf = |
waix - (Jx ray - Jy rax) /I |
| Final angular velocity of object b=wbf = | wbix - (Jx rby - Jy rbx) /I wbiy - (Jx rby - Jy rbx) /I |
The results for the three dimensional case are as follows: (see this page for code and derivation)
| General Case (between Perfectly elastic and Perfectly inelastic) | |||||
| impulse J = |
|
||||
| Final velocity of object a= |
Vai - J/Ma | ||||
| Final velocity of object b= |
Vbi - J/Mb | ||||
| Final angular velocity of object a=waf = | wai - [Ia]-1(J x ra) | ||||
| Final angular velocity of object b=wbf = | wbi - [Ib]-1(J x rb) |
Collision Response for unconstrained rigid bodies
Until now we have kept the rotation and linear components separate, it would be good if we could combine them into a single set of equations, I can think of two approaches: here we combine them using vectors and matrices. I would also like to try an approach using geometric algebra and conformal space but I have not made any progress with yet.
As already explained here, When unconstrained rigid bodies are floating round in free space, perhaps under the influence of forces, then each object might be represented by a state vector like the following:
Dynamics state vector for an object:
| θx |
| θy |
| θz |
| Px |
| Py |
| Pz |
| lx |
| ly |
| lz |
| mvx |
| mvy |
| mvz |
These values might be gradually changing with time in a way that can be described by simple linear equations. This would go on until two or more objects collide, this produces a step change in these variables, a discontinuity or singularity, when an impulse is transferred between the two objects in an infinitesimally small time. When such a collision occurs we need to calculate the new state vectors for each object. To do this we need to gather the following information which describes the collision:
Collision parameters:
| a | reference to object a | ||||||||||||||||||||||||||||||||||||
| b | reference to object b | ||||||||||||||||||||||||||||||||||||
| sva | state vector for object a - 12 dimensional vector as above | ||||||||||||||||||||||||||||||||||||
| svb | state vector for object b - 12 dimensional vector as above | ||||||||||||||||||||||||||||||||||||
| Newton-Euler matrix for object a |
This matrix is explaind here and combines
the following information:
|
||||||||||||||||||||||||||||||||||||
| Newton-Euler matrix for object b |
As above for object b |
||||||||||||||||||||||||||||||||||||
| n | A normal vector (dimension 3), this is a normal to the point of collision and shows the direction that the impulse is transferred. | ||||||||||||||||||||||||||||||||||||
| cfa, cfb | Optional coefficient of friction for each object |
Physics Assumptions
The following is an analytical approach to collisions, it assumes the collision occurs at a point contact between rigid objects. This means that the objects do not break or deform on collision. If these assumptions would cause too many errors, for instance modeling the deformations of a car in a crash, or if the analytical approach produces equations which are too complex then try a numerical approach to collisions.
The dynamics equations for a single object were covered in the previous page. Here we extend this analysis to two objects so that we can calculate the result of a collision between the objects. As explained in the previous page, we need to translate all values (inertia, force, movement, etc.) to world or common coordinates.
Linear momentum, angular momentum and energy is passed between the colliding shapes at the point of collision by means of impulse. Assuming that we know the velocities before the impact, and the point of impact, then one or more of the following might be used to help us calculate the velocities after the collision:
- Conservation of momentum - The total momentum of the whole system will be conserved. The momentum is a vector quantity so in the 3D case it is conserved in whatever x,y and z axis we choose.
- Conservation of energy - The total energy of the whole system will be conserved, but energy may be converted between kinetic energy and other types of energy. So we need to make assumptions about this. In a perfectly elastic collision then the kinetic energy is conserved, in an inelastic collision some of the energy associated with the approaching objects may be converted to heat.
- Calculation of Impulse - The impulse could be calculated which would allow us to work out the change in velocity of both objects.
Also there are different outcomes depending on the properties of the objects colliding:
- If the objects are perfectly elastic, they will absorb the kinetic energy of the collision as potential energy (like a spring) and then instantly convert it back to kinetic energy, so that the objects bounce off each other with a separating velocity equal and opposite to the approaching velocity.
- If the objects are perfectly inelastic, they will stick together and the final velocities of the two objects will be equal. In this case the total kinetic energy will be reduced and some energy will be converted into heat or other forms of energy.
- The objects may be somewhere in-between these two extremes. So we could introduce an elasticity factor for each colliding object which would give final velocities somewhere between these two extremes. Another complication is that this factor might be different in different dimensions, for instance objects may collide and slide against each other, so friction may also need to be taken into account.
Other concepts:
| Impulse is the integral of force over time, it is measured in Newton-seconds. For instance a force of one Newton applied over one second will change the momentum, a force of two Newton's applied over half of a second will have the same effect. For rigid body collisions we take this to its limit and apply an infinite force over an infinitesimally small time. This impulse is equal to the change in momentum of the colliding objects. Because we are talking about forces here, Newton's third law applies, and the impulse on the colliding objects will be equal and opposite. |
|
Once we start working in two and three dimensions, there is the possibility of rotation to include. This makes the general solution of a collision very difficult to work out (too difficult for me so far - but I'm working on it, can you help?). Rotation has similar laws to linear collisions, there are equivalents to Newtons laws for rotations and the total angular momentum of a system is conserved in the same way as linear momentum is conserved. However the following issues make the calculation of collision response difficult:
|
|
In a complicated collision, then friction may be involved. However friction (as opposed to elasticity) is only involved if there is a force, such as gravity, pushing the colliding objects together. |
Collisions in 3 dimensions is quite a complex problem, I'll start with 1 dimension first, then try to build up to 2 and then 3 dimensions.
- Rigid Body Collisions - deriving general equations
- Rigid Body Collisions - numerical solution
- collisions with deformations
Implementing this in program
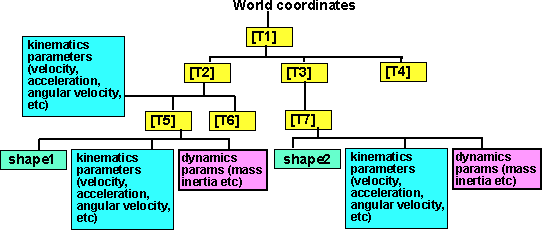
One issue I would like to keep in mind through these pages is, how do we use this theory in the program? It is proposed to include information about these physical properties in the scene graph.
For information about how to use this in the program see dynamics tutorial.
Determining the impact point
We not only need to detect that there has been a collision, we also need to find the point of impact relative to the centres of mass so that we can pass this information on to the collision response system.
Next Step and Further Reading
This page assumes that the collision has been detected in some way, this is discussed here.
To see how an algorithm for implementing collision response of a solid object see here.
To see a proposal for a structure to hold this collision response information see here.
Here is an off topic question, there seems to be 1 way an body can rotate in 2 dimensions and 3 ways that a body can rotate in 3 dimensions. How many ways could a body rotate in 4 dimensions?





