When we looked at vectors we saw that they must have two operations addition and scalar multiplication.
| operation | notation | explanation |
|---|---|---|
| addition | V(a+b) = V(a) + V(b) | the addition of two vectors is done by adding the corresponding elements of the two vectors. |
| scalar multiplication | V(s*a) = s * V(a) | a scalar product of a vector is done by multiplying the scalar product with each of its terms individually. |
These operations interact according to the distributivity property: s*(b+c)=s*b+s*c
In addition to these operations we can have other operations which we can apply to vectors such as the vector dot product:
Vector Dot Product
The dot product operation combines two vectors and produces a scalar output.
It is defined as follows:
Ax * Bx + Ay * By + Az * Bz
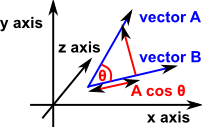
It is also given by A•B = |A| |B| cos(θ)
where:
- |A| = magnitude of vector A
- |B| = magnitude of vector B
- θ = angle between vector A and vector B
It is also equal to
A * projection of B on A
or
B * projection of A on B
The following is Java code for vector dot product.
double dot(sfvec3f other) {
return (x * other.x) + (y * other.y) + (z * other.z);
}
The following is managed C++ code for vector dot product.
Double sfvec3f::dot(sfvec3f* other) {
return (x * other->x) + (y * other->y) + (z * other->z);
}
This method will be used by the sfvec3f class.
Geometric Multiplication
Having two types of multiplication which give outputs that are not vectors is not altogether satisfactory. these operations are useful in that they have lots of practical applications. However, in mathematical terms, it would be better if we had a vector algebra that was 'closed' that is the outputs of the operations have the same form as the inputs.
This is not possible for vector algebra but it is possible if our elements are a superset of scalars, vectors, bivectors and higher order components. We can then define a general multiplication which is a combination of cross and dot multiplication.
This is Clifford Algebra/Geometric Algebra as described here.
Further Reading
Vectors can be manipulated by matrices, for example translated, rotated, scaled, reflected.
There are mathematical objects known a multivectors, these can be used to do many of the jobs that vectors do, but they don't have some of the limitations (for example vector cross product is limited to 3 dimensions and does not have an inverse).


