Geometric Algebra of 3 Dimensional Vectors G 3,0,0
| For 3 dimensions we can do the same thing, this time the results can be generated by 3 basis vectors, e1, e2and e3. Now multiplying out gives the following combinations: | 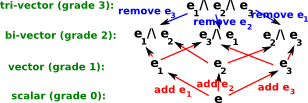 |
| basis | grade |
|---|---|
| e | scalar |
| e1,e2, e3 | vector |
| e1^e2, e1^e3 , e2^e3 | bivector |
| e1^e2^e3 | tri-vector |
In this case the bivector is 3D the same number of dimensions as the vector, the bivector has the same properties as the vector e1cept that a•a is a negative number for bivectors but it is a positive number for vectors (we will discuss multiplication rules later).
In this case the tri-vector has 1 dimension as for the scalar.
So in this case the multivector is made up of 8 scalar values.
This can lead to quantities that are quite tedious to write out therefore, in some cases, I will use the following abbreviations to make them easier to read and write:
| base value | numerical value | ||
|---|---|---|---|
full |
shortened |
||
| unit scalar | 1 | e | |
| unit length base vectors | e1 | e1 | |
| e2 | e2 | ||
| e3 | e3 | ||
| unit length base bivectors | e1^ e2 | e12 | e12 |
| e3^ e1 | e31 | e31 | |
| e2^ e3 | e23 | e23 | |
| unit length base tri-vector | e1^ e2^ e3 | e123 | e123 |
In the above table the base values are all unit length, they are like the 'i' operator in complex numbers or quaternions, these base values can then be multiplied by the numerical value which gives the actual value. Therefore any 3D multivector can be specified with these 8 numerical values which are just real (scalar) numbers.
In the case of 3D vectors the base values e1, e2and e3 could be thought of as unit vectors in the x,y and z direction. We could have used the notation ex, ey and ez but this might not fit so well when we work with higher dimensions. For this geometrical interpretation e1, e2and e3 could be any 3, mutually perpendicular, unit length vectors. In fact they don't have to be mutually perpendicular provided they are not all in one plane.
There are 3 combinations of outer products which cant be further reduced: e1^ e2, e3^ e1 and e2^ e3 , we could have chosen other combinations as base values but these are consistent and make the multiplication tables, below, more symmetrical. We can think of these as unit length base bivectors.
The order, starting at the scalar at the top down to the tri-vector at the bottom, also keeps the tables as symmetrical as possible, if we start from the top we are adding e1, e2and e3 if we start from the bottom we are removing e1, e2, e3 and this is important as explained in further pages.
So, using this notation, the general case of a 3D multivector is written:
e + e1 e1 + e2 e2 + e3 e3 + e12 e12 + e31 e31 + e23 e23 + e123 e123
This is similar to a complex number a + i b where:
- a is the real number part (similar to e in the multivector)
- i is the imaginary operator (similar to e1 in the multivector)
- b is the imaginary part of the number (similar to e1 in the multivector)
The multivector just has more parts to it.
So how do we choose which bivector bases that we use? For instance, why don't we use e13 instead of e31? We could have done this but, by using the values that we have then we get a correspondence with cross multiplication as shown here and also the multiplication table is symmetrical. Also all the e123 terms on the bottom left to top right diagonal are positive.
The following table is described and derived on this page. I have colour coded it as follows:
a*b |
b.e | b.e1 | b.e2 | b.e3 | b.e12 | b.e31 | b.e23 | b.e123 |
| a.e | 1 | e1 | e2 | e3 | e12 | e31 | e23 | e123 |
| a.e1 | e1 | 1 | e12 | -e31 | e2 | -e3 | e123 | e23 |
| a.e2 | e2 | -e12 | 1 | e23 | -e1 | e123 | e3 | e31 |
| a.e3 | e3 | e31 | -e23 | 1 | e123 | e1 | -e2 | e12 |
| a.e12 | e12 | -e2 | e1 | e123 | -1 | e23 | -e31 | -e3 |
| a.e31 | e31 | e3 | e123 | -e1 | -e23 | -1 | e12 | -e2 |
| a.e23 | e23 | e123 | -e3 | e2 | e31 | -e12 | -1 | -e1 |
| a.e123 | e123 | e23 | e31 | e12 | -e3 | -e2 | -e1 | -1 |
I have colour coded the elements to indicate which products commute and anticommute as follows:
| commutes |
| anticommutes |
You can check this by reflecting the cell you want to check in the leading diagonal (top left to bottom right) this is equivalent to swapping rows and columns, i.e. reversing the order of multiplication If the cell and the reflected cell are equal then it commute, if the cell is minus the reflected cell then it anticommutes.
If we changed any of the bivector bases, say by using e13 instead of e31, then we would loose the symmetry and also the correspondence with cross multiplication.
Cayley Table and Graph
If the basis vectors square to +ve then the Cayley table and graph are as follows:
| Cayley Table |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Cayley Graph | 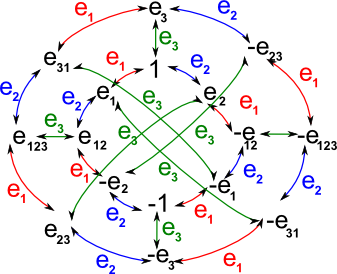 |
There are 3 generators since e1, e2 and e3 are the generators.
Even subalgebra
If we take the even subalgebra (scalar and bivector) then the Cayley table and graph are as follows:
| Cayley Table | Cayley Graph | |||||||||||||||||||||||||
|
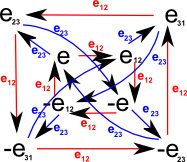 |
We only need two generators for the even sub-algebra, in this case we have chosen e12 and e23 but any 2 of the 3 bivectors.
Relationship to Cayley-Dickson Algebras
The relationship between the 8D Clifford algebras generated from 3D vectors and the 8D algebras (such as octonions) generated by the Cayley-Dickson doubling process is explained on this page.
| 8D Clifford algebras | octonions | |
|---|---|---|
| division algebra (inverse exists) | not always | yes |
| commutes | no | no |
| associative | yes | no |
Representing 3D solid bodies
So a geometric algebra, based on three dimensional vectors, has multivectors which have 8 scalar values (1 scalar, 3 vector, 3 bivector, 1 tri-vector). This would appear ideal for representing 3D solid bodies which have 6 degrees of freedom (3 for translation, 3 for orientation). Unfortunately however, the arithmetic of 3d multivectors can't be used to represent isometries (transforms representing translation and rotation). I guess that we could invent new operations to represent isometries with 3d multivectors but this would loose the properties described on this page. In order to represent 3D solid bodies using geometric algebra we need to use 4D multivectors as will be described on further pages. This means that we need 16 scalar variables to represent isometries, the same as a 4x4 matrix, which can also represent isometries and most people find matrices easier to understand. A number of people have told me that geometric algebra can be more powerful so I am investigation this on these pages. Perhaps a taste of the power of geometric algebra in this area can be found when we include the time variable as the scalar variable, this fits very well as the space we experience has 3 dimensions of distance and one dimension of time, using this we can derive the constants including energy and momentum, in one equation, as shown here.
Addition Rules
We just add corresponding terms. When adding blades of different grade then we cant reduce it further and we leave the + in the number.
For example:
3 + 4 e1 + 5 e23
added to
5 + 4 e1 + 3 e23
gives
8 + 8 e1 + 8 e23
Multiplication Rules
The main type of multiplication is geometric multiplication as follows,
Given a multivector with numerical values: a.e, a.e1, a.e2, a.e3, a.e12, a.e31, a.e23 and a.e123 multiplied by a second multivector with numerical values: b.e, b.e1, b.e2, b.e3, b.e12, b.e31, b.e23 and b.e123 then what are the resulting numerical values. Multiplying out each term gives the following result:
| e = | a.e * b.e | + a.e1 * b.e1 | + a.e2 * b.e2 | + a.e3 * b.e3 | - a.e12 * b.e12 | - a.e31 * b.e31 | - a.e23 * b.e23 | - a.e123 * b.e123 |
| e1 = | a.e1 * b.e | + a.e * b.e1 | - a.e12 * b.e2 | + a.e31 * b.e3 | + a.e2 * b.e12 | - a.e3 * b.e31 | - a.e123 * b.e23 | - a.e23 * b.e123 |
| e2 = | a.e2 * b.e | + a.e12 * b.e1 | + a.e * b.e2 | - a.e23 * b.e3 | - a.e1 * b.e12 | - a.e123 * b.e31 | + a.e3 * b.e23 | - a.e31 * b.e123 |
| e3 = | a.e3 * b.e | - a.e31 * b.e1 | + a.e23 * b.e2 | + a.e * b.e3 | - a.e123 * b.e12 | + a.e1 * b.e31 | - a.e2 * b.e23 | - a.e12 * b.e123 |
| e12 = | a.e12 * b.e | + a.e2 * b.e1 | - a.e1 * b.e2 | + a.e123 * b.e3 | + a.e * b.e12 | + a.e23 * b.e31 | - a.e31 * b.e23 | + a.e3 * b.e123 |
| e31 = | a.e31 * b.e | - a.e3 * b.e1 | + a.e123 * b.e2 | + a.e1 * b.e3 | - a.e23 * b.e12 | + a.e * b.e31 | + a.e12 * b.e23 | + a.e2 * b.e123 |
| e23 = | a.e23 * b.e | + a.e123 * b.e1 | + a.e3 * b.e2 | - a.e2 * b.e3 | + a.e31 * b.e12 | - a.e12 * b.e31 | + a.e * b.e23 | + a.e1 * b.e123 |
| e123 = | a.e123 * b.e | + a.e23 * b.e1 | + a.e31 * b.e2 | + a.e12 * b.e3 | + a.e3 * b.e12 | + a.e2 * b.e31 | + a.e1 * b.e23 | + a.e * b.e123 |
This result is derived here. It also explains the other types of multiplication such as inner and outer products.
Representing Transforms
One way to use multivectors is to represent transforms, to do this we need to show how to use it to map one point (vector) onto another point (vector), this table shows different ways to
| Translation type | possible representation | how to transform point |
| translation | vector | p + t |
| orthogonal (rotation) | quaternion 3*3 matrix |
q p q' [m]v |
| isometries (rotation + translation) | multivector | A p A -1 |
| linear (rotation, translation, scale (different for each dimension), reflection, shear, etc.) | 4*4 matrix | [m]v |
The various types of transformation are described on this page.
So in the case of multivectors we are proposing to translate the vector pin into the vector pout by using the equation:
pout = A pin A -1
where:
- A is a multivector representing the transform.
- pin is a vector representing a point before it has been translated.
- pout is a vector representing the same point after it has been translated.
Not every multivector has an inverse so, in order for this to work, we need to work with a subset of A that A -1 always exists (and solid body movement will always have an inverse). One condition that will ensure that an inverse always has an inverse is:
A A†= 1
where:
- A†is the 'reversal' of A which is defined on this page.
This is similar to unit length quaternions, where q conj(q) = 1 or orthogonal matrices where [m][m]t = 1
Another requirement is that if p is a vector then A p A -1 will also be a vector.
Are these two requirements related? Can we use this identity to relate them:
(A B)† = B† A†
Further Reading
You may be interested in other means to represent orientation and rotational quantities such as:
Or you may be interested in how these quantities are used to simulate physical objects: