These pages explain how geometric algebra can be used to represent geometric objects. We start with vectors (quantities with direction and magnitude) we then go on to combine these to give planes and higher order objects. The various types of element are discussed on this page.
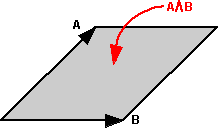
A vector can represent a line which starts at the origin and ends at some given point, a bivector can represent a plane, which in turn can represent a direction of rotation.
All of these quantities go through the origin, this is due to the linear nature of the algebra that we are working with, in many cases this is not a problem. For example, we often want to calculate rotations around the origin, if we need displacements from the origin it is often easiest to deal with these separately. It is possible to use geometric algebra to work with elements that do not go through the origin, this is explained on the pages that deal with projective and conformal space, but for now we will keep things simple and concentrate on elements that go through the origin.
Join
If we have two vectors then they define a plane (assuming the vectors are different from each other). note: for now all these quantities go through the origin. That is, there is only one plane which contains both vectors. This is similar to a union operation 'U' in set theory except that the plane contains not only the vectors A and B but also all the other vectors in that plane.
Join Example
Lets start with the simple case of the basis vectors e1 and e2. The join is e1^e2 this is a plane and can't be simplified further.
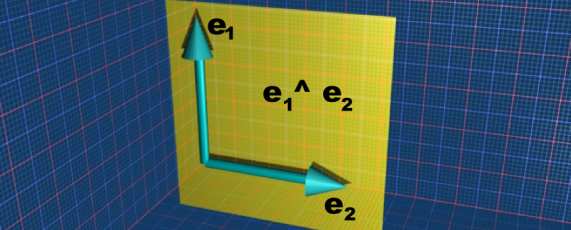
More about join on this page.
Meet
If we have two planes then they define a vector (assuming the planes are different from each other). That is along the line where the planes intersect so this is similar to the intersection operation in set theory.
Meet Example
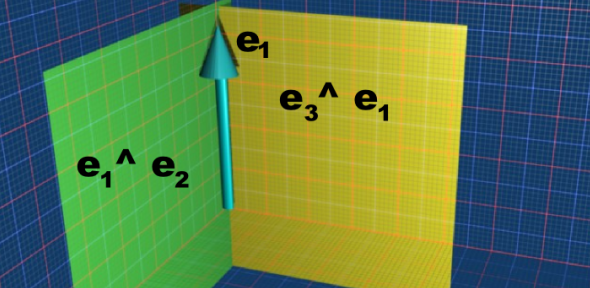
Lets start with the simple case of the basis bivectors e3^e1 and e1^e2. The meet is e1 we can see that this is the vector common to both planes.
Transforms
There are many types of translation that we can apply to our elements such as: rotation,scaling,translation,reflection, projection (parallel), projection (perpendicular) discussed in more detail on this page.
Perhaps the most useful is rotation, this is done using two geometric multiplications, 'sandwiching' the element being rotated.
We often need to transform points which, unlike the other types of elements discussed on this page, are displaced from the origin and then we want to rotate them around the origin.
