Description
On the previous pages we showed that from a two dimensional vectors we generate an algebra with 4 elements (e, e1, e2and e1^e2) .
| basis | grade |
|---|---|
| e | scalar |
| e1, e2 | vector |
| e1^e2 | bivector (in this case a scalar value) |
We can define a general 'number' in this algebra as a linear sum of these basis:
a + b e1 + c e2+ d e1^e2
We will call this 'number' a multivector, and for 2D vectors is is defined by the 4 scalar values here denoted by a,b,c and d.
| In order to understand the properties of this algebra we need to look at the arithmetic rules here. | 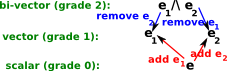 |
Such an algebra is the smallest, non-trivial clifford algebra so this may be a good chance to experiment with what we can change.
For instance, we can try changing the following aspects of the algebra:
- Do the basis vectors square to +ve, -ve or zero?
- Do we choose e1^e2 or e2^e1 as the basis bivector?
- Do the components, not on the leading diagonal, anti commute?
These options are discussed on this page.
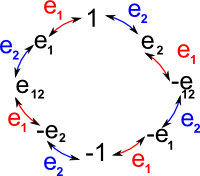
Cayley Table and Graph
If the basis vectors square to +ve then the Cayley table and graph are as follows:
Cayley Table |
Cayley Graph |
|||||||||||||||||||||||||
|
or as a hypercube:
|
There are 2 generators since e1 and e2 are the generators.
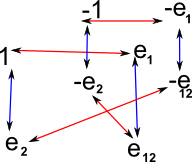
Even subalgebra
If we take the even subalgebra (scalar and bivector) then the Cayley table and graph are as follows:
Cayley Table |
Cayley Graph |
|||||||||
|
 |
This is isomorphic to the algebra of complex numbers, it has one generator: e12
Comparison of 2D multivector with Quaternion
Clifford algebras based on 2D vectors have 4 'dimensions' so how do they compare with quaternions which also have 4 dimensions? this is discussed on this page.