Clifford Algebra is the most general of this types of algebra. This page discusses the structure and rules of Clifford Algebra and how it can define other algebras like Geometric Algebra.
Clifford Algebra starts with a vector space of dimension 'n' and from it generates a vector space 'A' of dimension 2n or, another way to think about it, the vector space 'A' is made up of a number of smaller dimensional vector spaces.
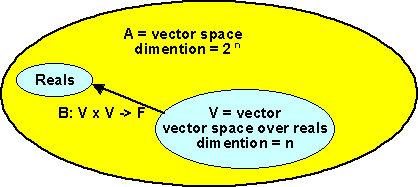
Because addition in clifford algebras is always defined by adding corresponding terms, this is relatively simple in that, it does not involve interaction between the various components.
So in order to define a Clifford Algebra we must define multiplication rules. In most types of algebra operations are 'closed', that is, when two elements of the algebra are combined the result is another element of the algebra. For example a complex number multiplied by another complex number will always produce another complex number. Clifford Algebra has a number of sub-algebras within one big algebra, however the sub-algebras are not closed within themselves only the overall algebra is closed. Apart from the case where n=0 which is just the real numbers all clifford algebras have a subset which are vectors, but multiplying a vector by another vector produces something that is not a vector, we can think of this as generating other types.
The number and dimension of the vector spaces have the structure of the binomial triangle. For any dimension 'n' of the vector space that we start with the vector spaces are given by the following sequence:
| n | 2n= | ||||||||||||||||||
| 0 | 1 | 1 | |||||||||||||||||
| 1 | 1 | 1 | 1+1 | ||||||||||||||||
| 2 | 1 | 2 | 1 | 1+2+1 | |||||||||||||||
| 3 | 1 | 3 | 3 | 1 | 1+3+3+1 | ||||||||||||||
| 4 | 1 | 4 | 6 | 4 | 1 | 1+4+6+4+1 | |||||||||||||
| 5 | 1 | 5 | 10 | 10 | 5 | 1 | 1+5+10+10+5+1 | ||||||||||||
| 6 | 1 | 6 | 15 | 20 | 15 | 6 | 1 | 1+6+15+20+15+6+1 | |||||||||||
| 7 | 1 | 7 | 21 | 35 | 35 | 21 | 7 | 1 | 1+7+21+35+35+21+7+1 | ||||||||||
| 8 | 1 | 8 | 28 | 56 | 70 | 56 | 28 | 8 | 1 | 1+8+28+56+70+56+28+8+1 | |||||||||
The dimension of the kth element is given by:
n!/(n-k)! k!
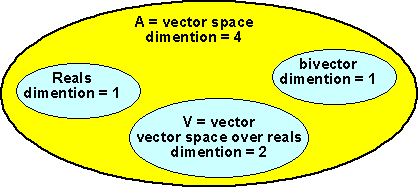
n=2
If we take the case where n=2 then we have a total dimension of 4, that is an element in this algebra can be represented by 4 scalar numbers, 1 for the real, 2 for the vector and 1 for the bivector.
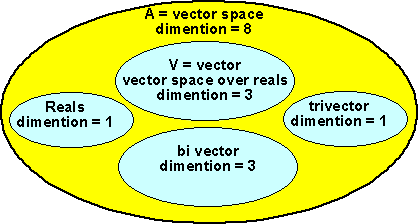
n=3
If we take the case where n=3 then we have a total dimension of 8, that is an element in this algebra can be represented by 8 scalar numbers, 1 for the real, 3 for the vector, 3 for the bivector and 1 for the trivector.