There is a 3D mulivector calculator at the end of this page.
The arithmatic on this page asumes the operands are a general case of a 3D multivector:
a.e + a.e1 e1 + a.e2 e2 + a.e3 e3 + a.e12 e1^ e2 + a.e31 e3^ e1 + a.e23 e2^ e3 + a.e123 e1^ e2^ e3
and a second multivector:
b.e + b.e1 e1 + b.e2 e2 + b.e3 e3 + b.e12 e1^ e2 + b.e31 e3^ e1 + b.e23 e2^ e3 + b.e123 e1^ e2^ e3
Adding multi vectors numbers
Just add each component independently as follows:
e = a.e + b.e
e1 = a.e1 + b.e1
e2 = a.e2 + b.e2
e3 = a.e3 + b.e3
e12 = a.e12 + b.e12
e31 = a.e31 + b.e31
e23 = a.e23 + b.e23
e123 = a.e123 + b.e123
This operation will be coded in the multi3d class (see
this class here).
When adding blades of different grade then we cant reduce it further and we leave the + in the number.
For example:
3 + 4 e1 + 5 e12
added to
5 + 4 e2 + 3 e12
gives
8 + 4 e1 + 4 e2 + 8 e12
Subtracting multi vectors numbers
Just subtract each component independently as follows:
e = a.e - b.e
ex = a.ex - b.ex
ey = a.ey - b.ey
ez = a.ez - b.ez
exy = a.exy - b.exy
ezx = a.ezx - b.ezx
eyz = a.eyz - b.eyz
exyz = a.exyz - b.exyz
This operation will be coded in the multi3d class (see
this class here).
Multiplying 3D multivectors numbers (geometric product)
The main type of multiplication, which is described here, is geometric multiplication.
So if we have a general case of a 3D multivector:
a.e + a.e1 e1 + a.e2 e2 + a.e3 e3 + a.e12 e1^ e2 + a.e31 e3^ e1 + a.e23 e2^ e3 + a.e123 e1^ e2^ e3
and a second multivector:
b.e + b.e1 e1 + b.e2 e2 + b.e3 e3 + b.e12 e1^ e2 + b.e31 e3^ e1 + b.e23 e2^ e3 + b.e123 e1^ e2^ e3
Since * is distributive over + we can multiply out the terms:
(a.e + a.e1 e1 + a.e2 e2 + a.e3 e3 + a.e12 e1^ e2 + a.e31 e3^ e1 + a.e23 e2^ e3 + a.e123 e1^ e2^ e3) * (b.e + b.e1 e1 + b.e2 e2 + b.e3 e3 + b.e12 e1^ e2 + b.e31 e3^ e1 + b.e23 e2^ e3 + b.e123 e1^ e2^ e3)
this gives the result:
This is derived from the multipication table:
a*b |
b.e |
b.e1 |
b.e2 |
b.e3 |
b.e12 |
b.e31 |
b.e23 |
b.e123 |
| a.e |
1 |
e1 |
e2 |
e3 |
e12 |
e31 |
e23 |
e123 |
| a.e1 |
e1 |
1 |
e12 |
-e31 |
e2 |
-e3 |
e123 |
e23 |
| a.e2 |
e2 |
-e12 |
1 |
e23 |
-e1 |
e123 |
e3 |
e31 |
| a.e3 |
e3 |
e31 |
-e23 |
1 |
e123 |
e1 |
-e2 |
e12 |
| a.e12 |
e12 |
-e2 |
e1 |
e123 |
-1 |
e23 |
-e31 |
-e3 |
| a.e31 |
e31 |
e3 |
e123 |
-e1 |
-e23 |
-1 |
e12 |
-e2 |
| a.e23 |
e23 |
e123 |
-e3 |
e2 |
e31 |
-e12 |
-1 |
-e1 |
| a.e123 |
e123 |
e23 |
e31 |
e12 |
-e3 |
-e2 |
-e1 |
-1 |
This multipication table is derived on this page.
alternative method
Some programs implement multiplication by using Eddington Basis
Eddington Basis for aMonad
E Number 1 : 0, 0, 0, *0
E Number 2 : 0, 0, 1, *1
E Number 3 : 0, 0, 2, *2
E Number 4 : 0, 0, 3, *3
E Number 5 : 0, 1, 2, *6
E Number 6 : 0, 1, 3, *7
E Number 7 : 0, 2, 3, *11
E Number 8 : 1, 2, 3, *27
Basis products for aMonad
E Number 1 : 1, 2, 3, 4, 5, 6, 7, 8, *0
E Number 2 : 2, 1, 5, 6, 3, 4, 8, 7, *1
E Number 3 : 3, -5, 1, 7, -2, -8, 4, -6, *2
E Number 4 : 4, -6, -7, 1, 8, -2, -3, 5, *3
E Number 5 : 5, -3, 2, 8, -1, -7, 6, -4, *6
E Number 6 : 6, -4, -8, 2, 7, -1, -5, 3, *7
E Number 7 : 7, 8, -4, 3, -6, 5, -1, -2, *11
E Number 8 : 8, 7, -6, 5, -4, 3, -2, -1, *27
Basis products for aMonad
E Number 1 : 1, 2, 3, 4, 5, 6, 7, 8, *0
E Number 2 : 2, -1, 5, 6, -3, -4, 8, -7, *1
E Number 3 : 3, -5, -1, 7, 2, -8, -4, 6, *2
E Number 4 : 4, -6, -7, -1, 8, 2, 3, -5, *3
E Number 5 : 5, 3, -2, 8, -1, 7, -6, -4, *6
E Number 6 : 6, 4, -8, -2, -7, -1, 5, 3, *7
E Number 7 : 7, 8, 4, -3, 6, -5, -1, -2, *11
E Number 8 : 8, -7, 6, -5, -4, 3, -2, 1, *27
Inner and Outer products

In addition to the geometric product there are two more types of multiplication used in Geometric Algebra. These extend and generalise the 'dot' and 'cross' products used in 3D vector algebra.
Inner product by a vector reduces the grade of a multivector. It is related to the dot product.
Outer product by a vector increases the grade of a multivector. It is related to the cross product.
Outer product
We want the outer product to be an extension of the vector cross product:
x = Ay * Bz - By * Az
y = Az * Bx - Bz * Ax
z = Ax * By - Bx * Ay
This gives a bivector which is mutually perpendicular to the vectors being multiplied. But how do we extend this so that we can multiply non-vectors? There are different definitions for the outer product so we need to be careful, if you use other websites or books you may find that they use different definitions. Here is the full 3D Outer multiplication table:
a^b |
b.e |
b.e1 |
b.e2 |
b.e3 |
b.e12 |
b.e31 |
b.e23 |
b.e123 |
| a.e |
e |
e1 |
e2 |
e3 |
e12 |
e31 |
e23 |
e123 |
| a.e1 |
e1 |
0 |
e12 |
-e31 |
0 |
0 |
e123 |
0 |
| a.e2 |
e2 |
-e12 |
0 |
e23 |
0 |
e123 |
0 |
0 |
| a.e3 |
e3 |
e31 |
-e23 |
0 |
e123 |
0 |
0 |
0 |
| a.e12 |
e12 |
0 |
0 |
e123 |
0 |
0 |
0 |
0 |
| a.e31 |
e31 |
0 |
e123 |
0 |
0 |
0 |
0 |
0 |
| a.e23 |
e23 |
e123 |
0 |
0 |
0 |
0 |
0 |
0 |
| a.e123 |
e123 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
This is explained here.
Inner product.
We want the outer product to be an extension of the vector dot product:
A • B = Ax * Bx + Ay * By + Az * Bz
This gives a scalar which depends on the angle between the vectors being multiplied, it is zero if the vectors are perpendicular and zero if the vectors are parallel. But how do we extend this so that we can multiply non-vectors? There are different definitions for the inner product so we need to be careful, if you use other websites or books you may find that they use different definitions. Here we will use the 'semi-commutative inner product' which has the following 3D Inner multiplication table:
a•b |
b.e |
b.e1 |
b.e2 |
b.e3 |
b.e12 |
b.e31 |
b.e23 |
b.e123 |
| a.e |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| a.e1 |
0 |
e |
0 |
0 |
e2 |
-e3 |
0 |
e23 |
| a.e2 |
0 |
0 |
e |
0 |
-e1 |
0 |
e3 |
e31 |
| a.e3 |
0 |
0 |
0 |
e |
0 |
e1 |
-e2 |
e12 |
| a.e12 |
0 |
-e2 |
e1 |
0 |
-e |
0 |
0 |
-e3 |
| a.e31 |
0 |
e3 |
0 |
-e1 |
0 |
-e |
0 |
-e2 |
| a.e23 |
0 |
0 |
-e3 |
e2 |
0 |
0 |
-e |
-e1 |
| a.e123 |
0 |
e23 |
e31 |
e12 |
-e3 |
-e2 |
-e1 |
-e |
This is explained here.
Division
We don't tend to use the 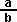 notation for division, since multivector multiplication is not commutative we
need to be able to distinguish between [a][b]-1 and [b]-1[a].
So instead of a divide operation we tend to multiply by the inverse.
notation for division, since multivector multiplication is not commutative we
need to be able to distinguish between [a][b]-1 and [b]-1[a].
So instead of a divide operation we tend to multiply by the inverse.
So the problem is, how to calculate the inverse of a multivector, this
is discussed here.
The following calculator allows you to calculate multivector arithmetic. Enter the values into the top two multivectors and then press "+ - or * " to display the result in the bottom multivector:

