For 'H' to be a subspace of a vector space 'V' it must have 3 properties:
- The zero vector of V is in H.
- For each 'u' and 'v' in H then v+u is also in H (closed under +).
- For each 'v' in H and scalar 's' then s*v is also in H (closed under scalar multipication).
Example of a Subspace
| V |
|
a vector space in 3 dimensions x,y and z | |||
| H |
|
a subspace of V formed by setting the z dimenstion to zero. |
Theorm
If v1…vp are in a vector space V, then span{v1…vp}is a subspace of V.
Lattice of Vector Subspaces
We can represent the relationships between a whole set of subspaces by a lattice structure (lattices are described on this page).
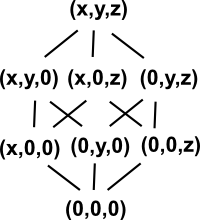
One way to encode this lattice structure of algebras is, as a Clifford algebra, as explained on this page.


