The angular momentum is the linear momentum times its distance from the axis of rotation.
When working out angular momentum its no use just summing the angular momentum's around the individual centres-of-mass of each body
* 
+ 
* 
= 
* + 
*
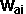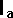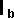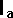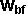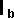
where:
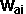| = initial angular speed of
body A |
= initial angular speed of
body B |
| = final angular speed of body
A |
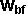= final angular speed of body
B |
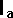= second moment of mass about
c-of-m of A  |
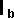= second moment of mass about
c-of-m of B |
Example 1
Imagine two bodies A and B of the same shape and mass. A is initially at rest, B is traveling toward A with no initial spin. So since they both started with with zero spin we might expect them to end up with equal and opposite spin.
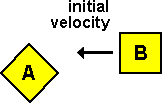
However that is not the case because A is hit in line with its own c-of-m so it gets no rotational component, however object B is not hit in line with its c-of-m so it will get a spin component.
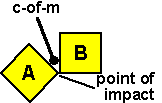
Therefore it is the angular momentum about the c-of-m OF THE WHOLE SYSTEM that is conserved?
I think this means that if, the point of impact is different from whole system c-of-m, then we need an extra term to include this extra rotational component about the system c-of-m.
But does this work? Consider another example:
Example 2
Two bodies with the same shape and mass, passing each other with equal and opposite speed and offset by distance r. Therefore the centre of mass of the whole system is stationary in the middle. Since the bodies are moving away, the moment of mass is increasing and the angle of rotation about the c-of-m is changing. But is the overall angular momentum remaining constant?
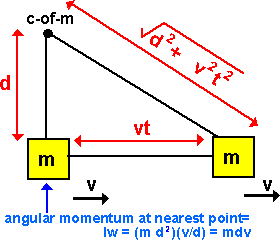
From the above diagram the angular momentum at the nearest point to the c-of-m = m d v
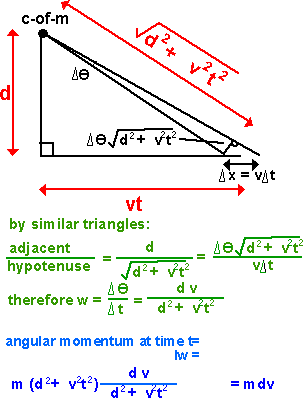
From the above after time t the angular momentum is still m d v
So angular momentum is conserved.
Thanks to Leo Wibberly for sending me this solution.
