For analytical approach to collisions see collisions

An approach would be to divide each object into equal sized cubes. Assuming the mass is uniformly dense, and the object is not rotating then, each cube will have the same momentum and energy. So the total energy and momentum is the sum of the energy and momentum of all the cubes. Conversely the energy and momentum of an individual cube is equal to the total energy and momentum divided by the number of cubes.
Rotation
The most difficult aspect of the analytical approach is, how to calculate the rotational component?
So how can we handle rotations numerically?
Although each cube in an object will have the same angular speed, but the angular momentum and energy of the object about its own centre of mass will be different from its momentum and energy about the objects centre of mass? As we have seen in the analytical approach this gets very complicated.
So, instead, can we just work in terms of the linear momentums and energies in the individual cubes?
So, for an object that is rotating, the linear momentums might look like this:
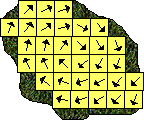
Each cube now has a different momentum vector, also as the object rotates the position and velocity vectors of each cube will be changing. However, if there are no external forces then, the total linear and angular momentum will be constant.
To get the overall linear momentum, at a particular instant, we can use:
{mom} = sum({vi})
| where: | |||
symbol |
description |
type |
units |
| {vi} | momentum vector for cube i | vector | |
| {mom} | overall linear momentum vector. | vector | |
To get the overall angular momentum we can use:
{ang_mom} = sum({p}x{vi})
| where: | |||
symbol |
description |
type |
units |
| {vi} | momentum vector for cube i | vector | kg m/s |
| {ang_mom} | overall angular momentum vector. | bivector | kg m2/s |
| {p} | position vector of the cube, relative to the centre of mass. | vector | m |
| x | cross product | ||
Kinematics
Since the vectors of each cube are constantly changing, we may need to calculate its position and momentum at any time, we could calculate these by:
- Using the conservation laws above.
- Integrate acceleration once to get velocity, then again to get position.
Note, numerical integration can gradually build up errors due to floating point errors, these errors can build up and case incorrect behavior as described here.
Collision
So how do we calculate the new momentum vectors after a collision? The tricky part is how to work out how the energy will transfer between linear and rotational energy. This may be easier if we work in linear terms for each cube. So when the objects collide there will be a large impulse generated:
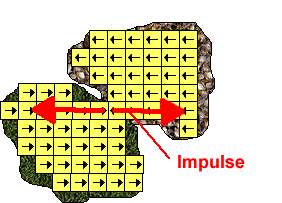
If we spread this amongst all the cubes this will give the movement for each cube:
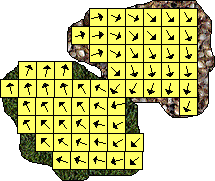
I think the next stage is to express the quantities like momentum and energy, using differential equations, in terms of the position in the object as described in FEM page.


