Table Top Physics - Collision

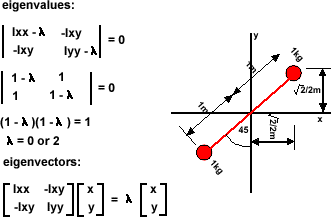
Next consider a rigid body with most of its mass at 45 degrees to the y plane.

Ixx = sum (y^2)dm = 0.5+0.5 = 1

Iyy = sum(x^2) dm = 0.5+0.5 = 1

Ixy = sum(x*y)dm =0.5+0.5 = 1

det[M] = Ixx Iyy - Ixy Ixy = 0.25-0.25 =0

diagram

x/y = Ixy /(Ixx - 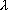lambda)

for 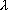lambda=0

x/y = 1/(1-0) = 1

normalising gives a unit vector at 45 degrees (along the line joining the masses).

for 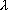lambda=2

x/y = 1/(1-2) = -1

normalising gives a unit vector at -45 degrees (at 90 degrees to the line joining the masses)

metadata block
see also:
Correspondence about this page

Book Shop - Further reading.

Where I can, I have put links to Amazon for books that are relevant to the subject, click on the appropriate country flag to get more details of the book or to buy it from them.

 

cover 3d Games: Physics -

 

cover Game Physics - This book has some useful stuff, its more of a textbook, not a step by step guide (although it does have a disc with a lot of C++ code). About the first third of the book is a physics textbook with theoretical exercises, the middle bit covers physics engine topics, and the last third of the book covers mathematical topics. I think I would use this book as a reference book to lookup the theory behind something I might be working on rather than a book to work through in order.

Commercial Software Shop

Where I can, I have put links to Amazon for commercial software, not directly related to the software project, but related to the subject being discussed, click on the appropriate country flag to get more details of the software or to buy it from them.

 

cover Dark Basic Professional Edition - It is better to get this professional edition

cover This is a version of basic designed for building games, for example to rotate a cube you might do the following:
make object cube 1,100
for x=1 to 360
rotate object 1,x,x,0
next x

cover Game Programming with Darkbasic - book for above software

This site may have errors. Don't use for critical systems.

Copyright (c) 1998-2023 Martin John Baker - All rights reserved - privacy policy.