The property of a geometry of being the same in all directions.
A symmetry operation will not change the object.
For example, if an object has mirror symmetry, then the operation of reflecting it on a mirror will not change it. But there are other types of symmetry than mirror symmetry which we will show on this page.
2D Symmetry
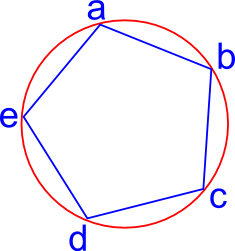
As an example in 2 dimensions, we could do an operation on this pentagon which maps:
a —» b
b —» c
c —» d
d —» e
e —» a
In other words we can rotate it by a fifth of a turn. Since the object is completely symmetrical in this way we will not be able to distinguish the new position from the original, they are identical. There are other symmetrical operations that we can do in this object, for instance, rotate it by two fifths of a turn.
3D Symmetry - Platonic Solids
In 3 dimensions there are platonic solids or regular polyhedron, which are solid 3 dimensional objects whose outer surface is made up of flat polygons, if we restrict ourselves to shapes whose faces are all the same then there are only 5 types.
| name | vertices | edges | faces | |
|---|---|---|---|---|
| Tetrahedron |  |
4 | 6 | 4 |
| Cube (Exahedron) |
 |
8 | 12 | 6 |
| Octahedron |  |
6 | 12 | 8 |
| Icosahedron |  |
12 | 30 | 20 |
| Dodecahedron |  |
20 | 30 | 12 |
There is a duality between pairs of these solid objects.
For instance
- The number of faces the dodecahedron = the number of vertices of icosahedron and visa versa.
- The number of faces the cube = the number of vertices of octahedron and visa versa.
Eulers Theorem on Polyhedron
v - e + f = 2
Where:
- v=number of vertices
- f=number of faces
- e=number of edges
Analysis of Rotation Symmetry
On this page we take the example of a cube and show how we can analyse its rotations using a permutation group.

