We are often introduced to determinants as constructs of matrices but determinants have a geometric interpretation as discussed here.
Independence of vectors (orthogonal basis)
Imagine that we have 3 vectors in 3D space, then we normalise these vectors and put them in a 3x3 matrix:
| x1 | x2 | x3 |
| y1 | y2 | y3 |
| z1 | z2 | z3 |
If these vectors are all in the same plane then the determinant of the matrix will be zero:
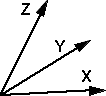
If these vectors are mutually perpendicular then the determinant of the matrix will be one (or minus one):
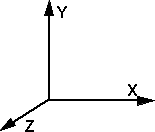
so the determinant allows us to determine if the vectors are independent so that they can span the space.
What we are doing here is defining a set of basis vectors in terms of another. In other words defining one coordinate system in terms of another coordinate system. This is the same as representing a transform as described here.
If |M| =1 then the transform represents a rotation (or an even number of reflections) from the original coordinate system.
If |M| = -1 then the transform represents an odd number of reflections from the original coordinate system.
If |M| is positive then the new basis vectors will have the same handedness, for instance, if the absolute coordinate system is right handed then the basis vectors will also form a right hand coordinate system.
If |M| is negative then the new basis vectors will have the opposite handedness, for instance, if the absolute coordinate system is right handed then the basis vectors will form a left hand coordinate system.
Volume enclosed by vectors
|M| is the volume enclosed by the vectors. However the sign is significant , it may be negative, if an odd number of coordinates are inverted the 'volume' will be negative.
This is the same as the tri-vector of a 3D clifford algebra.
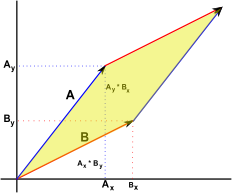
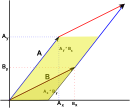
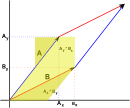
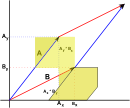
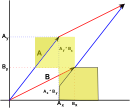
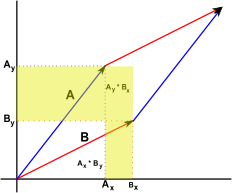
Two Dimensional Determinant
If we take two 2 dimensional vectors (shown here as red and blue) and take the area formed by the parallelogram between them. We then cut around bits of this parallelogram and rearrange it to give:
 |
|||
 |
 |
 |
 |
 |
|||
which gives an area which can be calculated as:
Ay*Bx - Ax*By
which in matrix terms is:
| det |
|
the determinant of the matrix formed from the vectors, note how the order of the vectors is important here or we will get a negative area.
Three Dimensional Determinant
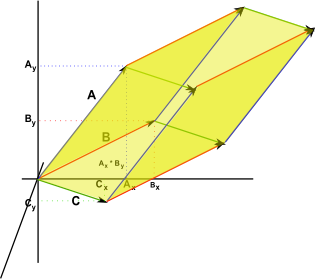
Its harder to do this graphically but we get
Ax By Cz + Ay Bz Cx + Az Bx Cy - Ax Bz Cy - Ay Bx Cz - Az By Cx
which in matrix terms is:
| det |
|
Which is the volume formed by the 3 dimensional parallelogram formed by the 3 vectors.
'n' Dimensional Determinant
In 'n' dimensions the determinant is the highest dimensional element (line, area, volume, hypervolume...) in that particular space.
In Clifford algebra terms it is the scalar multiplier of the pseudoscalar.

