This page explains various projections, for instance if we are working in two dimensional space we can calculate:
- The component of the point, in 2D, that is parallel to the line.
- The component of the point, in 2D, that is perpendicular to the line.
- A mapping from the 2D point to one dimensional space represented by the line.
- A mapping from the one dimensional distance along the line to the position in 2 space.
These transformations are related as we will discuss.
The following pages extend this topic:
To start with the simplest case consider a point projected onto a two dimensional line.
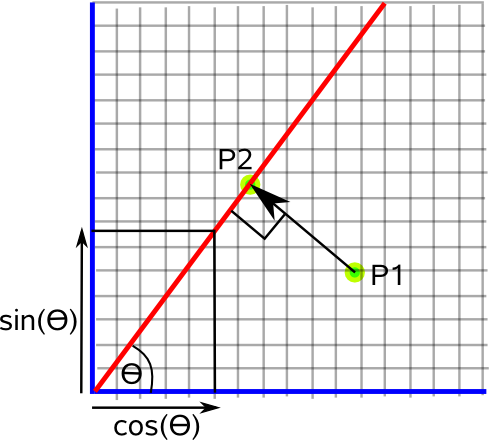
If we want to map the two dimensional space shown here onto the one dimensional space of the line we can use:
P2 = line • P1
where:
- P1 = vector representing a point to be transformed
- P2 = scalar representing point in terms of its distance along line.
- • = vector dot product.
- line = line represented by a normalised length vector (cos(θ),sin(θ)).
In matrix or tensor terms this would be:
| P2 = |
|
|
In other words we transpose the line vector and multiply it by the vector represented by the point in question.
In complex number terms this would be:
P2 = real(line' * P1)
where:
- P1 = point to be transformed P1x + i P1y
- P2 = scalar representing point in terms of its distance along line.
- real() = a function which takes the real part and sets the imaginary part to zero .
- line = cos(θ) + i sin(θ)
- line' = cos(θ) - i sin(θ)
One dimension to a line in two dimensions
We can also do the inverse transform, that is, take an input which is a scalar distance along a line and to map this to a two dimensional position on the line.
| P2 = |
|
* P1 |
where:
- P1 = scalar input representing a distance along the line
- P2 = vector representing point on the line.
Result left in 2 dimensions
What if we want to map the points onto a line but leave that line in two dimensional space (as is shown in the diagram above)? We can do this by mapping to a scalar value and then mapping back to two dimensions, that is, apply both of the above transforms in sequence.
We will use the notation:
P2 = P1 || line
That is the component of P1 that is parallel to the line.
In matrix or tensor terms this would be given by:
| P2 = |
|
|
|
Where, in this case,
- P2 = vector giving the position of the point after it is transformed onto the line.
Multiplying the terms gives:
| P2 = |
|
|
We can also calculate the perpendicular distance of the point from the line
We will use the notation:
P2 = P1 ![]() line
line
That is the perpendicular distance between P1 and the line.
this is given by:
| P2 = ( |
|
- |
|
) |
|
Which gives:
| P2 = |
|
|
Using Geometric Algebra Notation
We can repeat the above results using geometric algebra notation.
Mapping 2D to 1D
Mapping a point in 2 (or more) dimensions to a one dimensional (scalar) value to represent the distance along the line.
A first attempt at this would be A•B
where:
- A = vector representing a point.
- B = vector representing a line.
This gives a scalar as required, but it is not quite right unless B is unit length, otherwise we can use:
a = (A•B)/|B|
where:
- a = scalar length along line.
- A = vector representing a point.
- B = vector representing a line.
Mapping 1D to 2D
We can use scalar multiplication to get the two dimensional position from the scalar length along the line.
A = (a*B)/|B|
where:
- a = scalar length along line.
- A = vector representing a point.
- B = vector representing a line.
Parallel Component of a Point
We can calculate the parallel component of a point (A) to a line (B) by converting to a one dimensional distance along the line and that converting back to two dimensions. To do this we combine the above expressions as follows:
A || B = A•B * B/|B|2
Perpendicular Component of a Point
A ![]() B = (A x B) x B /|B|2
B = (A x B) x B /|B|2
Summary
Since (B•B) = |B|2 we can rewrite these expressions as:
- A || B = A•B * B/(B•B)
- A
 B = (A x B) x B /(B•B)
B = (A x B) x B /(B•B)
Higher Dimensions
We can also project onto a line in higher dimensions such as 3D, we just increase the dimension of the vectors that we are using.
- P1 = vector representing a point to be transformed, this will now be (P1x,P1y,P1z)
- line = line represented by a normalised length vector. This will now be (x,y,z) where x2+y2+z2=1.

