Euclidean Vector Space
Euclidean space is linear, what does this mean? One way to define this is to define all points on a cartesian coordinate system or in terms of a linear combination of orthogonal (mutually perpendicular) basis vectors.
So any point could be identified by:
P = α Va + β Vb +…
where:
- P = vector representation of a point.
- α, β,… = scalar multipliers (one for each dimension).
- Va, Vb,… = basis vectors (one for each dimension).
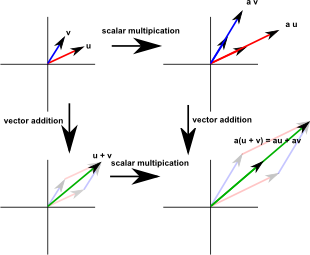
So we have two types of mathematical objects: scalars and vectors. The properties of such a space can be defined in terms of vector addition and scalar multiplication as defined by the following axioms:
| Associativity of addition | u + (v + w) = (u + v) + w |
| Commutativity of addition | v + w = w + v |
| Identity element of addition | v + 0 = v |
| Inverse elements of addition | −v |
| Distributivity of scalar multiplication with respect to vector addition | (u + v)a = ua + av |
| Compatibility of scalar multiplication with field multiplication | a(bv) = (ab)v |
| Identity element of scalar multiplication | 1v = v |
where:
- u,v,w… are vectors
- a,b … are scalars
In abstract algebra terms we can think of vectors as extensions to the field of real numbers as described on this page.
Quadratic Form
Euclidean space is quadratic, how can space be both linear and quadratic? We have already seen how vectors and scalar multiplication are linear, some aspects of Euclidean space are quadratic.
For instance the way that we measure distance (the metric) of a space. If we have a two dimensional Euclidean space, where a given point is represented by the vector: v= [x,y] then the distance from the origin is given by the square root of: x² + y². Other physical quantities such as the inertia tensor are also related to the square of the distance to a given point.
For more information about quadratic see this page or box on right.
Euclidean Metric
A metric is a function which determines the distance between objects. This depends on the coordinate system, for example we can talk about:
- A Euclidean metric, or
- A Riemannian metric
So the distance from the origin using a Euclidean metric is given by the square root of: x² + y²… This can be represented by the square root of v•v, in other words the root of the square of the vector from the origin to the point.
Alternatively we can use matrix notation, in this case the square of the distance is the column vector multiplied by its transpose.
|
|
=x² + y² |
This 'distance' quantity should be independent of the direction of the coordinate system. So lets check that when we rotate the coordinates the distance does not vary. We can easily rotate the column vector by multiplying by a rotation matrix:
|
|
So how do we rotate the row vector? We can use the rule for matrix multiplication:
[M1 * M2]t = [M2]t * [M1]t
where the t superscript means transpose. In other words, to multiply the transpose of two matrices we reverse the order and get the transpose of the whole thing:
|
|
t |
So making these two substitutions for the rotation vectors we have:
|
|
t |
|
|
=x² + y² |
but a rotation matrix times its transpose gives the identity matrix so the rotation matrices cancel out showing that the distance is independent of the orientation of the bases:
|
|
=x² + y² |
Units
We usually use 'metres' to measure distance.
Dot Product
Rules of dot products:
- v1•v2= v2•v1= |v1|•|v2|*cosθ
- (v1+v2)•v3= v1•v3 + v2•v3
- s*(v1•v2)= (s*v1)•v2 = v1•(s*v2)
- v1•v2 > 0 if and only if v1≠0
Bases
Since a vector is a quantity with magnitude and direction we can use a vector to identify the position of a point relative to the origin of our coordinate system.
If we don't happen to have a vector handy to specify our point we can specify a point as a linear combination of vectors.
For example, if we are working in two dimensions then we can determine the position from a linear combination of two different (non-parallel) base vectors.
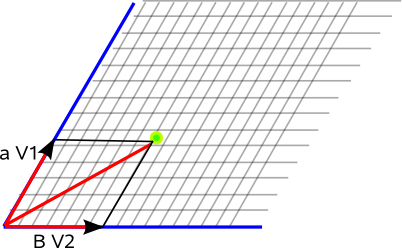
So any point could be identified by:
α Va + β Vb
where:
- α, β = scalar multipliers
- Va, Vb = basis vectors.
So the two scalar multipliers (α, β) can represent the position of the point in terms of our basis vectors.
I must say, when I first came across this idea of basis vectors, I was skeptical, if we already have a way to specify the basis vectors then why not use that method to specify the point? It seems a bit redundant and almost recursive. But the idea is useful (see the matrix version of the lookAt function) and it has a theoretical importance where in subjects like tensors and Clifford Algebras where we often want to define things in a purely geometric, coordinate free way.
Vector Space
Space has properties beyond the ability to specify the position of a point. For example, in Euclidean space, the distance between points on a solid object remain constant regardless of how that object is moved and rotated.
So some properties remain constant whatever coordinate system we use, we may want Pythagoras theorem to be be true independently of the coordinate system.
For instance in Euclidean Space, where Va and Vb are mutually perpendicular, we have:
(Va + Vb)² = Va² + Vb²
If we apply some transform to the space then we don't want this property to change with the coordinate system. If the space is linear then:
f(α Va) = α f(Va)
and
f(Va + Vb) = f(Va) + f(Vb)
which can be combined to give:
f(α Va + β Vb) = α f(Va) + β f(Vb)
Norm
Is a function which assigns length to a vector.
Three Dimensional Orthogonal Bases
If the basis vectors are orthogonal then they have some useful properties which can either be expressed in vector algebra or matrix terms:
Expressed in vector algebra terms
Any basis vector projected onto any other gives zero:
B1 • B2 = 0
B2 • B3 = 0
B3 • B1 = 0
Also, all the basis vectors are mutually perpendicular:
B3 = B1 × B2
B1 = B2 × B3
B2 = B3 × B1
Expressed in matrix terms
If we take these three basis vectors and put them together as 3 columns to form a 3×3 matrix [B] then the equivalent matrix equation combining all the above vector equations is:
[B][B]T = 1
We can easily prove these vector and matrix forms are equivalent by wring out the individual elements of the matrix and multiplying it out.
We can rearrange this dividing both sides by [B] to give,
[B]-1=[B]T
This is almost a complete expression of the properties of orthogonal bases, but not quite, we also need to include the fact that the bases are unit length and we are using a right handed coordinate system. To do this we need to add the fact that the determinant of this matrix is plus one:
det[B] = 1
We now have a complete definition of our orthogonal bases.
Mathematical Definition of Vector Space
addition of vectors
closure,associativity,commutativity,zero element
The general vector space does not have a multiplication which multiples two vectors to give a third. (although for n=3 or n=7 the cross product can be used although it is not commutative and it does not have an inverse).
There is also a dot product which combines two vectors to give a real (which we will call a scalar) this is associated with the metric of the vector space.
multiplication of a vector by a scalar(real number) to give another vector
distributivity,associativity,unity element.
Infinitely Large and Infinitesimally Small Vectors
Although this may seem a bit esoteric it can be very useful to represent points at infinity. This has applications in, say, perspective representation or denoting translations as rotations around infinity.
To illustrate the issue: imagine a vector P1 which happens to be (4,5). We now want to double it to a vector, P2, which has the same direction but is double the length (8,10) this is no problem. We now want to keep the same direction again but this time make it infinite length, the way we would denote this would be (∞,∞). Using this notation we have lost our representation of direction.

In order to get round this problem we use compactification as described on this page.
There is a similar issue with Infinitesimally Small Vectors, that is (0,0) contains no direction information. So if we are plotting direction as we vary a vector close to (0,0) its direction will vary wildly and at (0,0) it will be undefined. Some compact spaces, for example conformal space, can also eliminate this problem.

