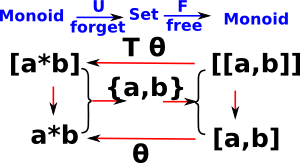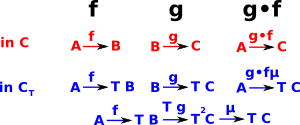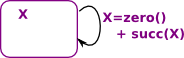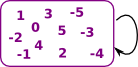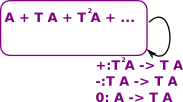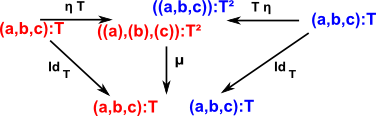Algebra for a Monad
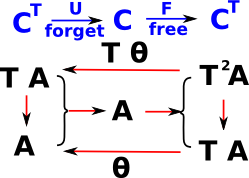
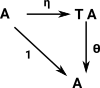
Given a monad: T: C -> C , 1 =>η T <=µ T denoted by the triple <T,η,µ>
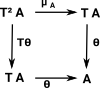
An algebra for a monad <T,η,µ> is an object A
C equipped with an 'action': a morphism θ:TA->A so that the following diagrams commute:
| Axioms of an algebra A: |
 |
|
 |
Relationship to an Algebraic Theory
If the monad T represents an algebraic theory.
Then an 'algebra for a monad' represents a model for the algebraic theory, that is, an implementation of it.
| Monad |
an algebraic theory |
Syntax |
Holds all the operations that may be needed. |
Let us form algebras |
| Algebra for a monad |
a model for the algebraic theory |
Semantics |
An implementation of those operations. |
Let us evaluate (collapse) algebras |
Informal Introduction
| We can think of the endofunctor of a monad in terms of an expression |
 |
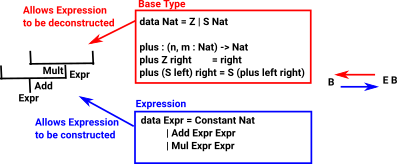We are first introduced to 'algebra' as a part of mathematics where we can use letters (variables) to stand in for numbers that are unknown or we don't wish to use the literal value. We can then use this to express axioms like: x+y =y+x.
Here we relate algebras to monads. The monad will allow us to build up expressions and the algebra will allow us to evaluate it back to a single value.
In order to construct a monad, in this case, we start with an endofunctor A -> T A. This takes a variable and gives us an expression in that variable.
Examples:
We can compose these by substituting one in the other, like this
So where x appears in the first we have substituted (x+2) which is the second.
We now have the two natural transformations:
Which gives us a monad.
On the remainder of this page we investigate questions such as:
- Are there other monads which model algebras?
- What is the link to adjunctions?
- Is there a similar structure for co-algebras?
Monads and Algebras
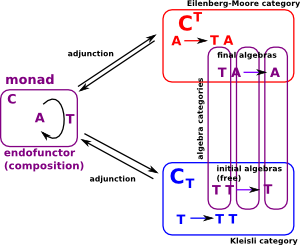
| There is a connection between monads, adjunctions and algebras. |
 |
An algebra can have two levels:
- An algebraic theory - defines function signatures and axioms.
- A model of that theory - defines the implementation of the functions.
Algebras and Coalgebras
Algebras have a structure based on products, so a subalgebra is a quotient. Coalgebras have a structure and substructure based on sum.
Monad as Algebraic Theory
A monad <T,η,µ> can represent an algebraic theory as might be given by function signatures and axioms.
Category of Algebras
We can generalise this concept to a category of algebras (alg T) where the objects are the morphisms θ:TA->A
Monadisity
Given any category 'C', is it an alg T for some T?
There is a whole category of algebras with two extremes:
- The Eilenberg-Moore algebra (CT) is terminal in this category of algebras. It has different objects but the same arrows as C.
- The Kleisli algebra is initial (CT)in this category of algebras. It has the same objects but different arrows as C.
Adjunctions and Algebras
Here we will talk about 'an algebra' to talk about specific mathematical 'equational theories' (The theory of fields is not equational because not every element has a multiplicative inverse).
An 'equational theory' is called a 'T-Algebra'. This gives rise to a free -| forgetful adjunction between sets and the category of models of the theory.
- forgetful functor U: T-Alg -> Sets
- free functor F: Sets -> T-Alg
The 'initial algebra' for an endofunctor P:S->S is a 'least fixed point' for P. Such algebras can be used in computer science to model 'recursive datatypes'.
F-algebras
F-algebras are discussed on this page.
Monads and Adjunction
Given a monad T on C is there an adjunction giving rise to it?
Every monad comes from an adjunction via its category of algebras
Example 1 - Set
| For a finite set we can have seperate constructors for each element. In the infinite examples below the underlying set is defined inductivly but since this example is finite then we only need 'X' on the left side of the equation only. |
 |
| |
Kleisli |
Eilenberg-Moore |
| |
initial |
terminal
one-point algebra |
| Object |
X = a() + b() + c() |
T X X |
| Arrow |
T = X X |
X->X |
| |
 |
 |
| Syntax |
|
|
| Axioms |
|
|
Example 2 - Natural Numbers
| If we start with the natural numbers and some endofunction on them, then we can generate the initial and terminal algebras. |
 |
| |
Kleisli |
Eilenberg-Moore |
| |
initial |
terminal |
| Object |
X = Zero() | Succ(X)
If we put in the usual notation for 'algebraic data types then we have to make:
- Zero=(1 -> N)
- Succ=(N -> N)
The algebraic type for natural numbers is:
N = 1+N
Although this notation is confusing in this case since, '1' represents zero and '+' represents disjoint union and not addition. |
T AA |
| Arrow |
T(X) = least fixpoint of above
Zero+Succ(Zero())+Succ(Succ(Zero()))+... |
A->A |
| |
 |
 |
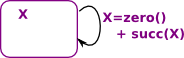| Axioms |
if X=Y
then succ(X)=succ(Y) |
0+A = A + 0 = A
A+B=B+A
(A+B)+C=A+(B+C) |
| |
The functions zero and succ generate a carrier set, this has a structure in that it is ordered. |
Any algebra that obeys the axioms can represent the natural numbers. |
Example 3 - Integers
| Now extend the natural numbers example by adding negative numbers. |
 |
| |
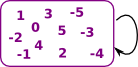Kleisli |
Eilenberg-Moore |
| |
initial |
terminal |
| Object |
A |
T AA |
| Arrow |
T |
A->A |
| |
 |
 |
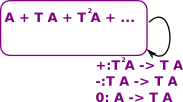| Syntax |
A=zero()
A=succ(A)
A=pre(A) |
0()->T
+(T,T)->T
-T->T |
| Axioms |
if A=B
then succ(A)=succ(B)
and pre(A)=pre(B)
pre(succ(A)) = A
succ(pre(A)) = A |
0+A = A + 0 = A
A+(-A) = 0
A+B=B+A
(A+B)+C=A+(B+C) |
| |
The functions zero,succ and pre seem to generate the elements. |
|
Example 4 - Rational Numbers
| Now extend the natural numbers example by adding negative numbers. |
|
| |
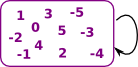Kleisli |
Eilenberg-Moore |
| |
initial |
terminal |
| Object |
X =
f(0) = 1
f(n+1) = ½ f(n) |
T AA |
| Arrow |
T |
A->A |
| |
|
|
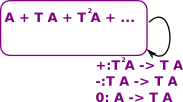| Syntax |
A=zero()
A=succ(A)
A=pre(A) |
0()->T
+(T,T)->T
-T->T |
| Axioms |
if A=B
then succ(A)=succ(B)
and pre(A)=pre(B)
pre(succ(A)) = A
succ(pre(A)) = A |
0+A = A + 0 = A
A+(-A) = 0
A+B=B+A
(A+B)+C=A+(B+C) |
| |
The functions zero,succ and pre seem to generate the elements. |
|
Example 5 - Algebra from Syntax
Can we create an algebraic theory from a (BNF) abstract syntax tree like this:
| BNF |
Element (Example) |
E ::= E | E '+' E | E '*' E | '-' E | N
N ::=
(0..9)+
where:
- E is an expression in N.
- N is a number.
|
 |
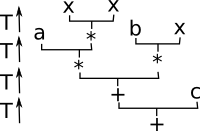| How can we construct an expression? Can we form a monad? |
 |
So a unit for a monad could be:
N -> E N
Can this construct an expression using this? This does not appear to specify where in the heirarchy of the expression where to put this value.
Stack
it is only a tree if your base functor is a product functor. When you have a sum functor as the base functor it more closely resembles a stack machine - http://stackoverflow.com/questions/13352205/what-are-free-monads
| We could perhaps represent this with using multicategories like this: |
 |
Example 6 - Words - Monad for Monoid
| On this page we discuss monoids in terms of a binary operation and an identity element, but there is another way to approach monoids (especially free monoids), that is as a singly linked list. |
 |
| We can convert between these notions of monoid using a 'fold' operation. |
 |
The underlying category has objects which are either:
- characters
- lists of characters
- lists of lists of characters
- … and so on.
The endo-functor 'T' maps from this object to itself, in this case it maps:
- a character to a list of characters
- and a list of characters to a list of list of characters
- and so on.
This endofunctor is equipped with two natural transformations:
- unit µ: 1 -> T
- multiplication (join) η: T×T -> T
Where,
- µ removes the inner set of brackets - takes a list of lists and joins the inner lists
- ηT adds brackets to each of the inner elements
- T η adds brackets around the outside of an instance.
|
 |
So from this we can see the effect of various transformations:
| x |
-T-> |
(x) |
|
T wraps element in list |
| x |
-ηx-> |
(x) |
|
η at x wraps element in list |
| (x,y) |
-T-> |
((x),(y)) |
|
T takes each element of list and wraps it in a sublist |
| (x,y) |
-ηTx-> |
((x,y)) |
|
η at T takes the whole list and wraps it in a sublist |
| (x,y) |
-Tηx-> |
((x),(y)) |
|
T•η at x takes each element of list and wraps it in a sublist |
| ((x,y)) |
-µx-> |
(x,y) |
|
µ removes brackets - takes a list of lists and joins the inner lists |
| (((x,y))) |
-µTx-> |
((x,y)) |
|
|
| |
-T-> |
|
|
|
| |
-T-> |
|
|
|
| |
-T-> |
|
|
|
| This satisfies the left and right triangle identities: |
 |
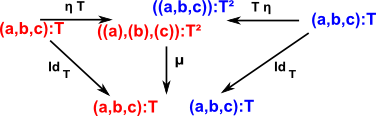| and the associative square: |
|
Example 7 - Monad on Poset
An endofunctor on posets models closure. Posets don't have loops, therefore defined by fixpoints.
Define T: P -> P
with
gives
T² <= T (that is it is idempotent) |
 |
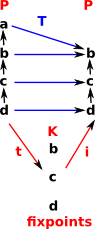Which gives an adjunction: t
i
This is discussed as an adjunction on page here.
Monads for Different Theories
| |
Monad for Monoid |
Monad for Small Categories |
|
| C |
List |
Graph |
|
| 1 |
empty list |
|
|
| T |
list of elements |
free category on a graph |
|
| T² |
list of list of elements |
|
|
| unit (in algebra not monad) |
wrap in a list |
identity functor |
|
| multiplication (in algebra not monad) |
flatten (remove inner brackets) |
composition of two functors |
|
| unit µ for monad |
|
|
|
| multiplication η for monad |
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
Computer Implementation of Algebra
More information about recursive types on this page.
Requires a carrier type to be defined then we need the algebra to be defined like this:
Monoid |
data MonF a = MEmpty | MAppend a a |
Ring |
data RingF a = RZero | ROne | RNeg a | RAdd a a | Rmull a a |
To make this into an expression we need a recursive definition :
Monoid |
data MonExpr = MEmpty | MAppend Expr Expr |
Ring |
data RingExpr = RZero | ROne | RNeg RingExpr |
RAdd RingExpr RingExpr | Rmull RingExpr RingExpr |
