On these pages we look at some basic principles of category theory and also how category theory relates to computation:
Graphs
As already explained on this page, category theory tends to use graphs (arrow diagrams) to represent the properties of a category. These diagrams naturally represent the properties of categories such as composing of arrows. So, since the arrows can be composed, why aren't our diagrams a complete mess of arrows with every object having a direct arrow to every other object? |
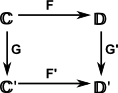 |
Well, first of all we suppress drawing every possible arrow, for example in the square above we could draw an arrow from C to D', but for clarity we don't draw it but leave it understood that we could if we needed to.
Secondly our diagrams often don't have loops. Any loop in the diagram could be fully interconnected by arrows but where there is no loop, as in the square above, there are arrows that are not implied. For example, between C' and D. When we are interested in diagrams commuting then we don't need loops.
That is not to say that diagrams never have loops. We often have a diagram with two objects, say A and B and arrows going in each direction. This can represent a relationship such as isomophism, equivalence or adjunction between them as described on this page.
The arrows represent morphisms (or functors etc.) or possibly a whole set of possible morphisms. Its a bit like variables? So we need to understand, for each arrow, what are the constraints on its possible values. Multiple possible morphisms are often represented by homsets.
Further topics
We also look at some specific topics in category theory such as:
 |
Functors |