see Wiki
 |
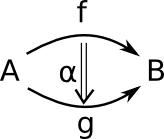
This blue area is intended to illustrate some general topological space (which may have holes in it). There could be many paths from the composition of paths A and B |
Higher Category Theory
In higher category theory diagrams may commute up to homotopy, but not on the nose, so higher homotopical information is needed to characterise the morphisms below it. (homotopy coherence)
A ( ∞ , 1) category is a category with
- n-morphisms where n may be unlimited and,
- these morphisms are invertible for n>1
Quasi-categories and Simplicial Sets
Quasi-categories can be represented by simplicial sets where:
- Points (0-simplices) represent the objects.
- Edges (1-simplices) represent the morphisms between these objects. These morphisms are directed (so is not a groupoid) and their composition is well-defined only up to 2-simplices.
- Triangles (2-simplices) represent homotopies between morphisms.
- So on for higher order faces. These higher order morphisms, above dimension 1, are weakly invertible and can also be composed, but the composition is well-defined only up to still higher order invertible morphisms.
 |
The triangle is intended to represent all the possible compositions of A and B that can be continuously deformed into each other. |
| We can combine these together so A is composed with B and also with C. |  |
 |
Or here B•A=D•C |
| If we compose a sequence of three morphisms we get homotopies between homotopies. |  |
 |
This is best shown in 3 dimensions where each morphism is shown in a different dimension. |
Nerve and Geometric Realisation
Nerve and geometric realisation are a pair of adjoint functors
The nerve is the right adjoint.
Weak Kan Complexes
Weak Kan complexes are a model for (infinity,1) categories.