Maths - Leibniz Equality

Overview

Roughly speaking Leibniz equality says that if we can't distinguish between two things then they are equal.

To put this into slightly more mathematical terms, elements are equal if they have the same properties (one value equals another if any predicate that holds of the first holds of the second).

This concept of equality corresponds to Martin-Löf identity.

further topics:

Leibniz Equality and parametricity
Leibniz Equality and extensionality
Leibniz Equality as a universal property
Leibniz Equality as an adjunction

but first an introduction:

Introduction to Leibniz Equality and Indiscerniblity of Identicals

If x=y then does F(x)=F(y)?

If F is well behaved (pure, total) then I think we would say that is true. What about the reverse?

If F(x)=F(y) then does x=y?

In general no, for instance if f is sine function and a=0 , b=2π then

sine 0 = sine 2π but 0≠2π

What if we change this to the condition that F(x)=F(y) for every valid F?

If F(x) and F(y) normalise to the same value for every F does x and y normalise to the same value?	Σ_a:AΣ_b:B(F(x)=F(y))
That is, if F . F(x)=F(y) then does x=y? This is true upto Leibniz equality. On the right I have drawn this like a fibre bundle which can be a good way of approaching it.
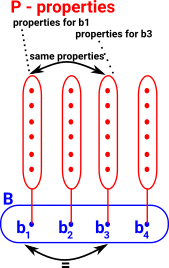Leibniz Equality in Category Theory Is there a universal property expressing Leibniz equality? It is related to a pullback (also called a fibre product)
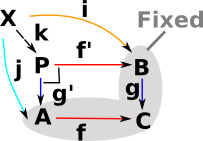Example in Number Expressions This generates pairs of elements <a, b> : P with a in A, b in B, such that f(a) = g(b). So the requirement for this square to commute generates in P all the possible pairs of numbers that are equal to each other. So, in the example on the right, 4 is a 'representative' for all the things it is equal to such as 2+2 and 3+1. Sometimes the notation [4] is used for the set of all the things it is equal to (although this notation could be confused with list). More about this on pullback page. This is definitional equality, how does this work for Leibniz equality?
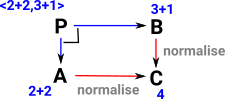Another example of a pullback comes from the theory of fibre bundles. Given a bundle map π : E -> B and a continuous map f : X -> B, the pullback (formed in the category of topological spaces with continuous maps) X ×_B E is a fibre bundle over X called the pullback bundle. The associated commutative diagram is a morphism of fibre bundles.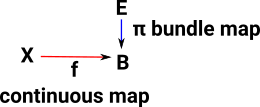
Or from ncatlab: In the category Set a ‘pullback’ is a subset of the cartesian product of two sets. The ‘pullback’ of this diagram is the subset X⊆A×B consisting of pairs (a,b) such that the equation f(a)=g(b) holds. A pullback is therefore the categorical semantics of an equation.

More information about fibre product on this page.

Is it also true upto definitional equality?

In Terms of Properties

Leibniz equality says that if two terms have the same properties (for all properties) then they are equal. How can we code this?

First lets try to express the proposition that if:

x=y

and some property of x say

p(x)

is true then p(y) is true

||| Leibniz Equality.
leib : (x:A ~= y:A) -> Type
leib (x ~= y) = (p:A->Type) -> p x -> p y

This function reurns a type thay is inhabited if p x implies p y. for all p.

Where:

~= represents Leibniz equality
x and y are variables or expressions.
p is a property, most likely an equation which depends on above variables.

Note: the compiler needs to be able to infer x and y and then infer the property.

It turns out that Leibniz equality is symmetrical, that is, if:

(x ~= y) -> p x -> p y

then:

(x ~= y) -> p y -> p x

So, if we have a function in each direction, do we have an isomorphism?

(x ~= y) -> p y ~ p x

Transport

This is known as transport. If x=y then their properties can be tranported across.

Transport turns path into equivelence.

Congruence

When programming we might represent properties as a function from a term to a type.

||| Equality is a congruence.
cong : {f : t -> u} -> (a = b) -> f a = f b
cong Refl = Refl

Idris code from Github

So if we have a property:	Prop : A -> Type
and if we have a proof that x=y where x and y are both of type A:	Refl : x=y
and we have a proof that Prop x is true:	Refl: Prop x
then Prop y is true:	Refl: Prop y

For example, in Idris, replace or rewrite (which has a nicer syntax)

||| Perform substitution in a term according to some equality.
replace : {a:_} -> {x:_} -> {y:_} -> {P : a -> Type} -> x = y -> P x -> P y
replace Refl prf = prf

Idris code from Github

In this context Leibniz equality is the same as propositional equality.

Proof

How could we prove that Leibniz Equality and M-L Identity are the same?

Example of Nat

One appoach is to represent each number by its Church encoding.

Consider all functions out of Nat. About the simplest, non-trivial type to map to we could think of is 2 (bool without any functions). So limit ourselves to:

Nat->Bool

We can use all possible functions of this type so, if we consider each natural number coded in binary there are function values of this type which pick out each digit.

So there is a list (ordered set) of such functions corresponding to each integer.

So there is a type family for every value of Nat.

Does this get us anywhere?

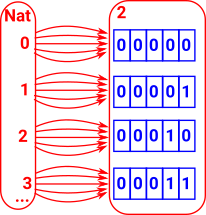Leibniz Equality and Parametricity

T : Type ->Type
TA = (X: Type) -> (A->X) -> X

types A and T A are isomorphic

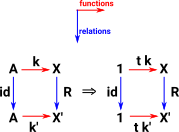paramT : (t: TA)->(X X' : Type) (R:X->X′->Type) ->
    (k:A->X) (k':A->X') (kR: (a:A) -> R(k a) (k' a)) ->
	R (t X k) (t X' k')

Leibniz Equality and Extensionality

Two functions are equal if they map equal values to equal results.

ext : {A: Type} {B:A->Type} {f g: (a:A)->B a} -> ((a:A) -> f a=g a)->f=g

Pullback as a Type

Is given by the dependent sum over the dependent equality type ncatlab:

P=Σ_a:AΣ_b:B(f(a)=g(b))

Leibniz Equality as an Adjunction

Leibniz Equality

The identity of indiscernibles is a principle that states that there cannot be separate (non-equal) objects or entities that have all their properties in common.

Given any x and y,

then x = y if and only if, given any predicate P, P(x) if and only if P(y).

(P(x) if and only if P(y)).

Leibniz Equality and Propositional Equality

In this context Leibniz equality and propositional equality are the same. There are conversions which allow us to prove one equality from the other.

In the special case where we have parametricity and functional extensionality then Leibniz equality is isomorphic to propositional equality although we are working with intentional type theory so we don't require that.

Here we model predicates of elements of 'A' as a type family 'C' over it.

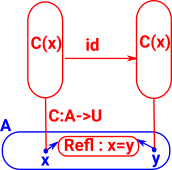Here we not only consider whether x=y but also the evidence for it given by p.

That is, we distinguish between the way things are equal. To do this we work in terms of function 'f'.

f : Π_x,y:A Π_p:x=y C(x) -> C(y)

Given a family C: Π_x,y:A (x =_Ay) -> U

and a function c: Π_x:A C(x,x,Refl)

there is a function f : Π_x,y:A Π_p:x=y C(x,y,p)

such that f(x,x,Refl) ≡c(x)

This gives rise to the elimination rule 'J' for propositional equality.

Γa:T		Γb:T		Γa=b		Γc(x) : C(x,x,Refl)		ΓC(x,y,x=y):Type
ΓJ (a=b,c) : C(a,b,Refl)

An Example in Natural Numbers

How can we prove that n=n+0 where n is a natural number?

To do this we would have to be able to constuct an equality type like this:

Refl:(n=n+0)

Is this definitionaly equal? For that to be the case then both sides of the equation 'n' and 'n+0' would have to normalise to the same thing. So does 'n+0' normalise to 'n'? This would depend on the implementation details but lets assume here that it doesn't.

So we need to prove its propositionally equal.

A is Nat

C is n -> (n=n+0)

Identity (Propositional Equality) Constructor

If we have an identity type		x = x : Type
then we can construct it with a simple constructor with no parameters		Refl : x = x

That is, if x=x is inhabited by Refl that constitutes a proof that x=x.

However this hides a lot of complexity, if we use the same symbol on both sides of the equation - what does that mean? We might say that the meaning comes from the deconstuctor but how is this all implemented?

In some ways we could think of rewrite as like a second constructor for an equality type. So it behaves a bit like an inductivly defined type where Refl can construct a definitional equality on its own but requires the help of rewrites to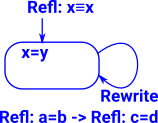

Identity (Propositional Equality) Deconstructor/Eliminator

There are also two possible deconstructors/eliminators known as J and K.

(K does not apply to some flavors of type theory)

In the same way that, in Leibniz equality, equal terms have equal properties we can now consider properties of equalities.

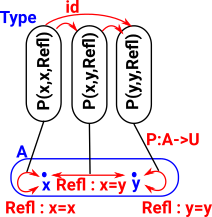Axiom J

The first part 'P' generates a property/type/proposition for every pair of terms which are equal:

(P : (a,b:t) -> (a=b) -> Type)

The next part shows that an element of each of these types (Refl) can be constructed and are therefore 'true':

((a:t) -> P a a Refl)

The result gives the value of the property for all equal terms.

((a,b:t) -> (p:a=b) -> P a b p)

J : (P : (a,b:t) -> (a=b) -> Type) ->
    ((a:t) -> P a a Refl) ->
    ((a,b:t) -> (p:a=b) -> P a b p)
J P h a a Refl = h a

Axiom J allows the posibility of many equality constructors Refl (although the single name and the pattern matching rules in Idris would prevent that).

If we want to specifically prevent the posibility of multiple Refl constructors then axiom K applies.

axiom K is discussed on the page here.

Equality Type Constructor

The equality type only has one constructor which is Refl (short for reflexive).

If we have an equation, such as 1+1=2, this can be constructed using Refl only if the left and right of the equation is the same. We think of this constructor as proof of that the equation is true.

If we have an identity with a variable, such as (x:Nat) -> x = x + 0, then we need to be able to generate a Refl for every value of x. For information about how to do this see the page here.

Equality Type eliminator

This goes in the opposite direction, that is, start with an equality type and take it apart somehow. The equality type eliminator, traditionally called J has two parameters:

A function P which generates a type family. This gives a type for every pair of elements.	(P : (a,b:t) -> (a≡b) -> Type)
A proof of equality for equal elements.	((a:t) -> P a a Refl)

From these parameters we can then generate the following function:

((a,b:t) -> (p:a≡b) -> P a b p)

Reflexivity from Eliminator

This is trivially true.

Symmetry from Eliminator

from here

symm : a ~~ b -> b ~~ a
symm {a} {b} a_is_b = 
  let f = J symm_P symm_P_for_refl
      f2 = the (a~~b -> b~~a) $ f a b a_is_b
    in f2 a_is_b
  where 
     symm_P : (a,b:t) -> (a~~b) -> Type
     symm_P a b x = a ~~ b -> b ~~ a

     symm_P_for_refl : (a:t) -> symm_P a a (refl_ a)
     symm_P_for_refl a = the (a ~~ a -> a ~~ a) $ id

We want to prove that a ~~ b implies b ~~ a

So we make a ~~ b -> b ~~ a a property of the Leibniz equality. This is saying that if a and b are equal then a can replace b and b can replace a.

symm_P : (a,b:t) -> (a~~b) -> Type
symm_P a b x = a ~~ b -> b ~~ a

Transitivity from Eliminator

from here

infixl 50 @-
(@-) : a ~~ b -> b ~~ c -> a ~~ c
(@-) {a} {b} {c} a_is_b = 
  let f = J (trans_P c) (trans_P_for_refl c)
      f2 = the (a ~~ b -> b ~~ c -> a ~~ c) $ f a b a_is_b
    in f2 a_is_b
  where
     trans_P : (c : t) -> (a,b:t) -> (a~~b) -> Type
     trans_P c a b x = a ~~ b -> b ~~ c -> a ~~ c

     trans_P_for_refl : (c : t) -> (a:t) -> trans_P c a a (refl_ a)
     trans_P_for_refl c a x = the (a ~~ c -> a ~~ c) $ id

tran : a ~~ b -> b ~~ c -> a ~~ c
tran = (@-)

We want to prove that a ~~ b and b ~~ c -> implies a ~~ c

So we make x ~~ c (being equal to c) a property of the Leibniz equality. This is saying that if a and b are equal and a is equal to c then b must also be equal to c.

trans_P : (c : t) -> (a,b:t) -> (a~~b) -> Type
trans_P c a b x = a ~~ b -> b ~~ c -> a ~~ c

Rewrite from Eliminator

from here

transport_P : {t : Type} -> (a, b : t) -> a ~~ b -> Type
transport_P {t} a b p = (P : t -> Type) -> P a -> P b

transport : {t : Type} -> (a, b : t) -> a ~~ b -> (P : t -> Type) -> P a -> P b
transport {t} a b a_eq_b P p_a = J {t} transport_P transport_for_refl_a a b a_eq_b P p_a
  where
    transport_for_refl_a : {t : Type} -> (a : t) -> (transport_P {t} a a (refl_ a))
    transport_for_refl_a a _ = id

We want to prove that a ~~ b implies P a -> P b

So we make P a -> P b a property of the Leibniz equality. This is saying that if a and b are equal then P a must be equal to P b so P a implies P b.

transport_P : {t : Type} -> (a, b : t) -> a ~~ b -> Type
transport_P {t} a b p = (P : t -> Type) -> P a -> P b

Logic Rules

Leibniz rule

q: a=b

T : A -> Set

t: T a

subst _A:a,b q T t : T b

computation rule

subst _A:a,a (refl a) T t = t: T a

Leibniz equality

if every property of x implies the same property
of y then x=y.

p: x-> Prop

p x -> py

x=y

In Set Theory More on page here.		Two sets are equal if they contain the same elements (Principle of Extensionality). If the set has structure then that would also have to be equal in some way.
In Category Theory More on page here.		Often when comparing types we need some loser way of considering that two types are essentially the same. Isomorphism is frequently the most appropriate type of equality. This is defined using a category theory way, that is, by external morphisms.
In Type Theory More on page here.	vec(x)=vec(x+0)	In M-L type theory the Identity type is often used. If things are equal in this way they can be interchanged when used in computer programs.
In Type Theory More on page here.		In Homotopy Type Theory (HoTT) there is a different way to get isomorphism from equality. That is to allow types to be equal in many ways.

Maths - Leibniz Equality

Overview

Introduction to Leibniz Equality and Indiscerniblity of Identicals

Leibniz Equality in Category Theory

Example in Number Expressions

In Terms of Properties

Transport

Congruence

Proof

Example of Nat

Leibniz Equality and Parametricity

Leibniz Equality and Extensionality

Pullback as a Type

Leibniz Equality as an Adjunction

Leibniz Equality

Leibniz Equality and Propositional Equality

An Example in Natural Numbers

Identity (Propositional Equality) Constructor

Identity (Propositional Equality) Deconstructor/Eliminator

Axiom J

Equality Type Constructor

Equality Type eliminator

Reflexivity from Eliminator

Symmetry from Eliminator

Transitivity from Eliminator

Rewrite from Eliminator

Logic Rules

EuclideanSpace

This Page

Related Subjects

Equality