Rewrite
Lets start by trying to prove commutativity of Nat addition: a + b = b + a.
We have already seen this proof derived here. On that page the proof was derived in a 'Type Driven Development' sort of way (filling in holes and so on). Here we are taking a complimentary, more theoretical approach in order to get an intuitive understanding of constructs and functions such as 'rewrite'.
| Here is the proof from Prelude.Nat although I've changed its name so that I can avoid conflicts when experimenting with it. |
|
|
For now we want to concentrate on the first case where the left parameter is Z.
|
|
This calls plusZeroRightNeutral from Prelude.Nat which is rewritten to produce our proof:
So how does this work? How does this apply the proof of plusCommutative in this proof?
| (plusZeroRightNeutral right) returns this: | Refl:(right + Z = right) | |
| but this is the goal we want to get to: | Refl: Z + right = right + Z |
So we are rewriting something of type right + Z = right to get to the goal Z + right = right + Z. However the code does not tell us how it is doing this. When we look at the difference between the goal and what we have we can see that we need to apply Z + right = right to transform a proof of one equation into another.
We can make this more explicit (and therefore more understamdable to someone reading the code) by using the ==> construct like this.
|
|
But rewrite is syntactic suger, how is it actually implemented?
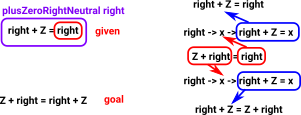
Another Example
As a simple example to explore the proof capabilities in Idris lets look at proving that adding zero does not alter a number.
As we have already seen, plus pattern matches on its first operand so:
'plus Z x' normalises to 'x' so proof is trivial: |
test1 : x=plus Z x test1 = Refl |
However 'plus x Z ' does not normalise to 'x' so we try using just Refl we get the following error: Type mismatch between plus x 0 and x |
test2 : x=plus x Z
test2 = Refl
fails |
We therefore need to give the compiler some help to prove this second case.
Perhaps the simplest way to think about what what we are trying to do here is to keep moving 'S' outside of the plus until we end up with (plus Z Z) which normalises to Z. |
|
| So we need to recursively call a function like this until all terms apart from Z are moved out of the plus: |
|
Generalising to other Nat Number Proofs
In order to prove something for all natural numbers, that is involving a variable like x:Nat, we need to use proof by induction. That is, we need to prove that,
- Its true for x=Z
- If its true for x then its also true for S x
In our case these translate as:
- plus Z Z = Z
- if plus x Z = x then plus (S x) Z = (S x)
The first one is trivial, the second one needs a proof like this:
inductiveStep: (x : Nat) -> x = (plus x Z) -> S x = plus (S x) Z)
Books & Papers about Agda
inductiveStep
| So our proof by induction would be of this form using recursion: |
|
All we have to do is implement inductiveStep.
In order to prove (x : Nat) -> x = (plus x Z) -> S x = plus (S x) Z) there are some proofs that are available to us:
We can increment both sides of an equation and it will still remain true. This is just a version of 'cong' which is specific to Nat. |
|
|
| We can move 'S' outside the plus. |
|
As shown, Idris can do these without any help. So we only need to combine tem to get what we want:
| So here is a full proof: |
|
The 'moveSOutside' has not been called explicitly because Idris can just apply that rule.
| in fact we don't need to state these steps in the proof explicitly, Idris can infer them. All we need to do is call the built-in function 'cong' . |
|
Using 'rewrite'
We have seen that the easiest way to prove this example is to use the built-in 'cong' function. However in more complicated examples this will not be the case. So, I think its worth seeing how to prove it using 'rewrite', this may help us with more complicated examples.
'cong' works by doing the same thing to both of an equation, however we may want to subtitute an individual variable in which case we need to use 'replace' or 'rewrite' .
So lets try using rewrite to prove this example.
Here is a proof using rewrite. Similar to a proof in libs/prelude/Prelude/Nat.idr |
|
The problem is that the above proof does not give the reader of the code many clues about how it actually works.
I think it is rewriting the first 'n' in 'S n = S n' to 'plus n Z'
| So we could make this a bit more explicit like this: |
|
|
| I have tried to represnt this as a diagram here: | 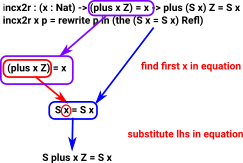 |
Using Match Syntax
There is a nicer syntax for explicitly giving the type of Refl shown above (more about match syntax on this page)
| Example using match syntax: |
|
The above syntax can be extended further, using <==, like this:
Z + n = n + Z could easily be proved from what we have already proved: Z + n = n and n + Z = n but instead this proof uses match syntax
|
|
For other examples of match syntax see:
prop : (x : Nat) -> Type
prop x = (plus x Z) = x
moveSOutside1 : (x : Nat) -> S (plus x Z) = (plus (S x) Z)
moveSOutside1 x = Refl
moveSOutside2 : (x : Nat) -> (plus (S x) Z) = S (plus x Z)
moveSOutside2 x = Refl
incBothSides : x = y -> S x = S y
incBothSides Refl = Refl
incx : (x : Nat) -> x = (plus x Z) -> S x = S (plus x Z)
incx x p = rewrite p in Refl -- rewrites x to plus x 0 in S x = S (plus x Z)
incxr : (x : Nat) -> (plus x Z) = x -> S (plus x Z) = S x
incxr x p = rewrite p in Refl -- rewrites plus x 0 to x in S x = S (plus x Z)
-- following fails with Type mismatch between plus x 0 and x
--incxb : (x : Nat) -> x = (plus x Z) -> S x = S (plus x Z)
--incxb x p = Refl
incx2 : (x : Nat) -> x = (plus x Z) -> S x = plus (S x) Z
incx2 x p = rewrite p in (the (S (plus x 0) = S (plus x 0)) Refl)
-- rewrites plus x 0 to x in (S (plus x 0) = S (plus x 0))
incx2r : (x : Nat) -> (plus x Z) = x -> plus (S x) Z = S x
incx2r x p = rewrite p in (the (S x = S x) Refl)
-- rewrites x to plus x 0 in (S x = S x)
-- following fails with Type mismatch between plus x 0 and x
--incx2b : (x : Nat) -> x = (plus x Z) -> S x = plus (S x) Z
--incx2b x p = Refl
-- rewrite__impl : (P : a -> Type) -> x = y -> P y -> P x
doNothing : (x : Nat) -> (plus x Z) = x -> (plus x Z) = x
doNothing x pr = rewrite__impl prop (the (x = x) Refl) pr
--doNothing2 : (x : Nat) -> (plus x Z) = x -> S (plus x Z) = S x
--doNothing2 x pr = rewrite__impl prop (the (x = x) Refl) pr
-- prove if x = (plus x Z) then S x = (plus (S x) Z)
-- we might be able to prove this by first proving:
-- if x = (plus x Z) then S x = S (plus x Z)
----------------------------------------------------------
--replace
-- Replace is defined like this:
-- ||| Perform substitution in a term according to some equality.
-- replace : {a:_} -> {x:_} -> {y:_} -> {P : a -> Type} -> x = y -> P x -> P y
-- replace Refl prf = prf
-- What I am trying to do here is to take the following proof which uses
-- rewrite and use replace instead:
total plusZeroRightNeutralRW : (x : Nat) -> (plus x Z) = x
plusZeroRightNeutralRW Z = Refl
plusZeroRightNeutralRW (S n) =
rewrite plusZeroRightNeutralRW n in (the (S n = S n) Refl)
-- rewrites (plus n Z) to n in (S n = S n)
--
-- instead of (S n = S n) I tried (S (plus n Z)) = S n) and ((plus (S n) Z) = S n)
-- and (S n = (S (plus n Z))) and (S n = (plus (S n) Z))
-- but they did not work. I got Type mismatch between n and plus n 0
--
-- Looking at this function it is not self explanatory, its not clear:
-- * What is the type of Refl ?
-- * What is the property P ?
--
-- So how do we change it to use replace? First try to use
-- rewrite__impl : (P : a -> Type) -> x = y -> P y -> P x
--
--total plusZeroRightNeutralRI : (x : Nat) -> (plus x Z) = x
--plusZeroRightNeutralRI Z = Refl
--plusZeroRightNeutralRI (S n) =
-- rewrite__impl prop (the (S n = S n) Refl) (plusZeroRightNeutralRI n)
--
--total plusZeroRightNeutralRI : (x : Nat) -> (plus x Z) = x
--plusZeroRightNeutralRI Z = Refl
--plusZeroRightNeutralRI (S n) =
-- rewrite__impl prop (the (S n = S n) Refl) (plusZeroRightNeutralRI n)
--
--total plusZeroRightNeutralRI : (x : Nat) -> (plus x Z) = x
--plusZeroRightNeutralRI Z = Refl
--plusZeroRightNeutralRI (S n) =
-- rewrite__impl prop ?t1 ?t2
--
--*proof> :t t1
-- n : Nat
-- y : Nat
--------------------------------------
--t1 : S n = y
--*proof> :t t2
-- n : Nat
-- y : Nat
--------------------------------------
--t2 : plus y 0 = y
--
-- this requires the second parameter to be S n = n
-- but rewrite__impl prop (the (S n = n) Refl) (plusZeroRightNeutralRI n)
-- means unifying n and S n would lead to infinite value
--
--total plusZeroRightNeutralRI : (x : Nat) -> (plus x Z) = x
--plusZeroRightNeutralRI Z = Refl
--plusZeroRightNeutralRI (S n) =
-- let y = S n in
-- rewrite__impl prop (the (y = S n) Refl) (plusZeroRightNeutralRI n)
--
-- So how do we change it to use replace?
--
--total plusZeroRightNeutralRep : (x : Nat) -> (plus x Z) = x
--plusZeroRightNeutralRep Z = Refl
--plusZeroRightNeutralRep (S n) =
-- replace {P = prop} (plusZeroRightNeutralRep n) (the (S n = S n) Refl)
-- |
-- 134 | replace {P = prop} (the (x = (S n)) Refl) plusZeroRightNeutralRep n
-- | ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
-- When checking right hand side of plusZeroRightNeutralRep with expected type
-- plus (S n) 0 = S n
-- When checking an application of function replace:
-- Type mismatch between
-- S n = S n
-- and
-- x = S n


