Model Theory
All the flavours of model theory rest on one fundamental notion, and that is the notion of a formula φ being true under an interpretation I. (Wilfrid Hodges)
Theory
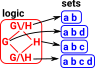
| In model theory a 'theory' is a set of first-order sentences, for instance: |
|
x.(x+0=x)In this diagram we have a box for each set of these sentances: The arrows mean implies. A set with more sentances can imply a set with less sentances because we are using Intuitionistic logic so we don't use the excluded middle rule. So if a sentance is not included in a set it doesn't mean its false it just means we are not saying anything about it. I have left out arrows if they are given by composing the above arrows. |
 |
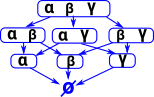| There is more we can imply from these sentances because α and γ implies β so we can add the red arrows: |  |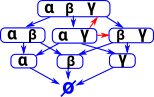
| In a similar way we can imply α from β and γ. We can't however imply γ from β and α. |  |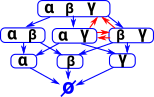
| If there is an implication arrow going in both directions we can treat the sets as being the same. So here I have put them in the same box: |  |
Model of Theory
There can be multiple models of any given theory
Interpretation
The variables are given values which make the sentances true.
Define a structure B using structure A.
see internal language of a category on page here.
Proofs in Different Theories
We can look at proving things in different theories, such as,
- Set Theory
- Type Theory
- Topology
- Homotopy Type Theory
- Category Theory
In many areas, such as set theory, we use a logic over the theory. When proving things we usually use Intuitionistic logic (see page here). Although there is also a connection between set theory and boolean logic which can be seen nicely in Venn diagrams. |
 |
Logic and Type Theory
| 'It is useful to distinguish between the internal type theory of a category and the internal logic which sits on top of that type theory. The type theory is about constructing objects, while the logic is about constructing subobjects.' | see ncatlab |
 |
In type theory, types can represent both the structure and the logic within type theory. |
Logic and Category Theory
See topos theory
Equality
| In Set Theory More on page here. |
 |
Two sets are equal if they contain the same elements (Principle of Extensionality). If the set has structure then that would also have to be equal in some way. |
| In Category Theory More on page here. |
 |
Often when comparing types we need some loser way of considering that two types are essentially the same. Isomorphism is frequently the most appropriate type of equality. This is defined using a category theory way, that is, by external morphisms. |
| In Type Theory More on page here. |
vec(x)=vec(x+0) | In M-L type theory the Identity type is often used. If things are equal in this way they can be interchanged when used in computer programs. |
| In Type Theory More on page here. |
 |
In Homotopy Type Theory (HoTT) there is a different way to get isomorphism from equality. That is to allow types to be equal in many ways. |
Equality
| In Set Theory More on page here. |
|
Two sets are equal if they contain the same elements (Principle of Extensionality). If the set has structure then that would also have to be equal in some way. |
| In Category Theory More on page here. |
|
Often when comparing types we need some loser way of considering that two types are essentially the same. Isomorphism is frequently the most appropriate type of equality. This is defined using a category theory way, that is, by external morphisms. |
| In Type Theory More on page here. |
vec(x)=vec(x+0) | In M-L type theory the Identity type is often used. If things are equal in this way they can be interchanged when used in computer programs. |
| In Type Theory More on page here. |
|
In Homotopy Type Theory (HoTT) there is a different way to get isomorphism from equality. That is to allow types to be equal in many ways. |
Equality
| In Set Theory More on page here. |
|
Two sets are equal if they contain the same elements (Principle of Extensionality). If the set has structure then that would also have to be equal in some way. |
| In Category Theory More on page here. |
|
Often when comparing types we need some loser way of considering that two types are essentially the same. Isomorphism is frequently the most appropriate type of equality. This is defined using a category theory way, that is, by external morphisms. |
| In Type Theory More on page here. |
vec(x)=vec(x+0) | In M-L type theory the Identity type is often used. If things are equal in this way they can be interchanged when used in computer programs. |
| In Type Theory More on page here. |
|
In Homotopy Type Theory (HoTT) there is a different way to get isomorphism from equality. That is to allow types to be equal in many ways. |
Next
A more axiomatic approach to model theory requires:
