Category theory usually only takes equality upto isomorphism.
Here it might be interesting to work out if we can use pullbacks to represent definitional equality. see these pages:
|
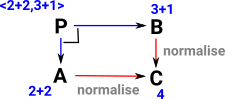 |
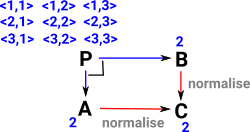
To explain this, imagine we have a set with three elements: 1,2 and 3. To find the equalities take all 9 combinations as tuples (that is, take product with itself). The ones where the left and right parts of the tuple are equal are the ones where this diagram commutes. That is <1,1> , <2,2> and <3,3>. |
 |
Can this thinking be extended to isomorphism instead of equality?
And can this be extended to Leibniz equality? That is, can we include proofs in this framework? |
 |
Discussed more on these pages: