Functions (mappings)
A function (or mapping) φ from a set 'A' to a set 'B' is a rule that assigns to each element 'a' of A' exactly one element 'b' of B. This is written:
φ: A -> B
Domain and Codomain
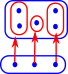
Domain This is the set which is the source of the function. |
 |
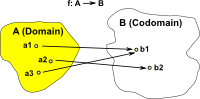Codomain This is the set which is the destination of the function. |
 |
Total Functions
Function which give an output for every possible value of the domain.
See injective function below.
Partial Functions
On this page we will mostly assume that every element in the domain maps to an element in the domain, however this is not the case for partial functions.
Examples of partial functions, in the real numbers, are:
- x->1/x (not defined for x=0)
- x->sqrt(x) (not defined for negative numbers)
This is also interesting in computing where a function may represent a computation. Where this computation is very complicated it may not be possible to be sure that every input to the function will produce a valid result.
The mathematics of partial functions is discussed further on the page here.
Injective, Surjective and Bijective Functions
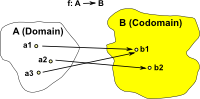
Injective function Every element in the domain is mapped to a unique element in the codomain. There may be elements in the domain that are not used. (size of domain <= size of codomain) |
 |
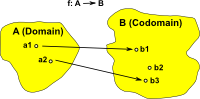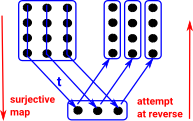
Surjective (onto) Elements in the domain may be mapped to the same element in the codomain but every element in the codomain is targeted. (size of domain >= size of codomain) |
 |
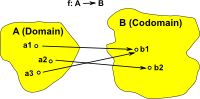Bijective function Every element in the domain is mapped to a unique element in the codomain and every element in the codomain is mapped to a unique element in the domain. (size of domain = size of codomain) |
 |
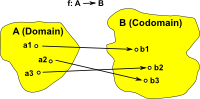Ways to Define a Function
- By specifying an algorithm.
- By specifying a set of ordered pairs. (In ZF set theory everything is a set). Either by specifying each pair or by a comprehension.
An important feature and a definition of functions is that a given input produces a unique output:
if <x,y>
f and <x,z>f then y=z
Ways to Define Equality of Functions
The (ZF) set theory way to define a relation is as a set of ordered pairs.
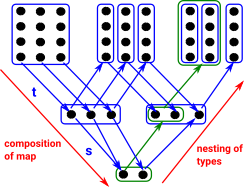
Composition of Functions
If we apply a function 'g' to and element x and then apply function h' to the result we get a combined function: (g o h)(x)
where:
- o represents the composition of these two functions.
In other words we have:
(g o h)(x) = h(g(x))
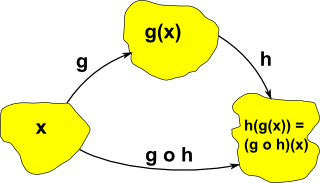
Function composition is always associative
(f o g)o h = f o (g o h)
Morphisms
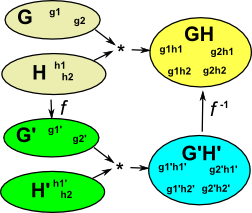
A morphism is a function f between sets with structure (such as group, ring or fields) that preserve some element of the structure.
For instance :
f(g * h) = f(g) * f(h)
Types of Morphisms
| morphism homomorphism |
general form, same meaning as homomorphism. |
| isomorphism | a morphism where the inverse f-1 is also a morphism. f-1(g * h) = f-1(g) * f-1(h) |
| automorphism | a isomorphism onto itself |
| endomorphism | a morphism onto itself |
Examples
Morphisms between Lattices on page here.
Image and Kernel
See short exact sequence.
| Image |  |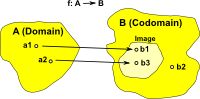
Kernel The set of all elements 'x' of a structure 'X' such that f(x) is the identity element of structure Y. |
 |
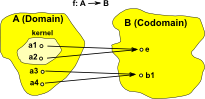Coimage the coimage of a morphism f: A -> B is the quotient: coim f = A/ker(f) |
 |
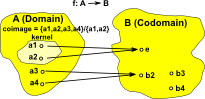Cokernel the cokernel of a linear mapping of vector spaces f : cokernel = B/im(f) |
 |
Composition of Maps and Nested Types
First look at how we might approximate reversing a map and then extend this to reversing a composition of maps. We can't reverse a surjective map exactly but instead of mapping back to invividual elements we can map back to sets. This generates equivalence classes or fibre bundles (or, in type theory, dependent types). |
 |
 |
Here we try to reverse two functions t and s composed together. Now we get nested equivalence classes or (or, in type theory, nested dependent types). |
- More about maps on this page.
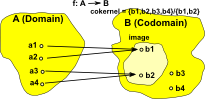Orbit and Stabiliser
see Sylow theory
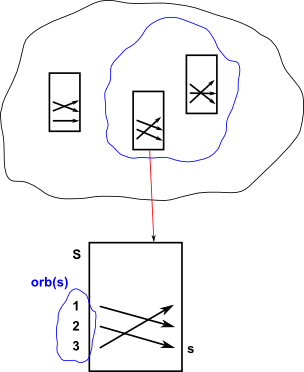
Orbit
orb(s) - When a group G acts on a set S, the orbit of any s in S is the set of elements of S that G arrows can reach from s.
orb(s) = {φ(s) | φG}
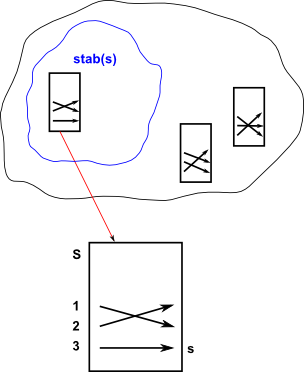
Stabiliser
stab(s) - The stabilizer of an element s in S is the set of group elements g that don't move s. A configuration s in S is called stable if no actions move s.
stab(s) = {φG | φ(s)=s}
Types of Map
| notation | example | meaning |
|---|---|---|
A B |
Map / Morphism / Function between mathematical structures that relates or preserves the structures in some way. May be injection, surjection or bijection (injection can be specifically indicated see below) | |
a  b |
A function in terms of elements of the structures aA, bB |
|
 |
A function that is valid if all the functions drawn as solid lines are valid | |
 |
injective morphism (embedding) | |
 |
canonical map - map of G onto factor group G/H where H is a normal subgroup of G |
More notation on this page.
More about category theory on this page.
