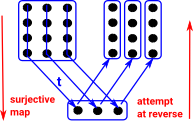
Dependent Product Types
| Dependent product types are an extension to function types. Ordinary function types are defined in terms of a fixed type for both the domain and codomain. | isZero: Nat -> Bool
Z=true
S n = false |
| This pseudo code is intended illustrate a function where the type of the output depends on the type of the input: | crazyFunction (b:Bool) -> (if b then Nat Else String)
true=1
false="fail" |
| More likely the output types would be more related to each other. For example, type families such as vectors where vectors of different length are different types: | data Vect : Nat -> Type -> Type where Nil : Vect Z a (::) : a -> Vect k a -> Vect (S k) a |
Other Approaches
Dependent types can be thought of as either:
- Type 'B' which depends on an element of another type 'A'. That is B(a) where a:A. In sets this looks like indexing.
- A family 'B' of types.
- A Fibre Bundle.
- In homotopy terms a dependent product looks like a path where ordinary types are points.
- In computer programs they provide a sort of meta level capability to types in that terms can be used at compile time and not just runtime.
- Logic - when extended to predicate logic we get quantifiers which give this structure
A common example of dependent types is vectors (see Idris library).
So we have a whole family of types. This type family is like a 3-layer hierarchy with the type family at the top level, below this are the individual types for each length, then at the bottom level are the elements consisting of the vectors. |
 |
Another way to think of this is as an example of the mathematical concept of a fibre bundle. A type such as Nat, has internal structure. With dependant types there is structure between types, shown here as an arrow (::) between Vect(1) and Vect(2) for example. So if normal types are thought of as points in topological space then dependent types can have paths between the points. |
 |
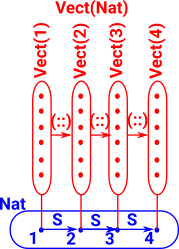Dependent Sum Types
As with dependent products there are different ways to characterise dependent sum types.
Here the type of the second element of the tuple (product type) depends of the first element. So instead of a function (exponential type) we have a tuple (product type). |
((b:Bool), (if b then Nat Else String)) an element of this type might be: (false,"fail") |
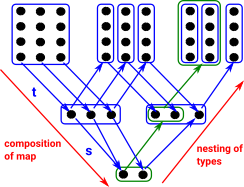
Dependent Product and Dependent Sum Types
There are two constructs of dependent types:
|
 (above diagram adapted from diagram in Thorsten Altenkirch paper) |
Each of these can be related to non-dependent types in two ways (blue and red lines in diagram above).
As extensions to non-dependent types:
- A dependent sum type is a product type definition (tuple) where the second type definition depends on the first.
- A dependent product type is a function type definition where the second type definition (output type) depends on the first (input type).
Note: this involves terms in the type definition (checked at compile time as opposed to run time).
As indexed types:
| Here we extend the binary product type to a product of multiple terms. In order to select a particular projection it is helpful to consider these types as indexed so the projections can be represented as a function from a term to a type: i -> Bi. |  |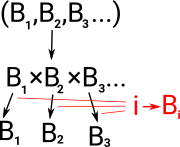
| Similarly the binary sum type can be extended to a sum of multiple terms. In order to use the type it is helpful to have an index to know what it is so the type can be represented as a product of a term and a type: i×Bi. |  |
This describes dependent types as a type indexed over a set. The theory of fibres (on page here) gives us a way to generalise this set to a more general type.
Notation
A dependent product type can be denoted like this: Πa : AB(a) Where:
Terms of this dependent product type can be denoted like this: x |
A dependent Sum type can be denoted like this: Σa : AB(a) Where:
Terms of this dependent sum type can be denoted like this: (x , B(x)) |
The dependent product term is the whole family of types so 'x' in x
B(x) is a variable whose value is not specified. The dependent sum term is one element in the family of types so 'x' in (x , B(x)) is a specific value.
So it makes sense that it is a function in one case and a product in the other case. In set theory a function is a set of pairs.
Constructors & Eliminators for Dependant Types
The constructors and eliminators for dependant types are the same as for ordinary types. We can have a similar construct to Nat or any other type constructor. The difference is, instead of constructing a 'Type', we construct a function or a product:
| Ordinary Type | Dependant Sum Type | Dependant Product Type | |
|---|---|---|---|
| What is constructed or eliminated: | Type | (a:A, U) | a:A -> U |
| Where 'U' means 'universe' that is a type whose elements are types. In Idris this is just denoted by Type and the hierarchy issues are hidden. | |||
| To make clear the dependence on 'a' we can notate it like this: | Type | (a:A, B(a)) | a:A ->B(a) |
In addition to its usual potentially recursive structure each constructor can refer to the dependant value 'a'. So its like having a type constructor over the normal constructors.
Example VectHere the constructors Nil and (::) construct an element without having to explicitly construct an element of the middle layer such as Vect 2 elem. |
 |
For further discussion about constructors and eliminators see this page.
